Confira aqui vários exercícios resolvidos sobre tronco de cone, onde podemos trabalhar com a ideia de área e volume.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria espacial.
Bom estudo!
Questão 1 (PM RJ – IBFC 2012). Um cone reto é seccionado por dois planos paralelos a sua base e que dividem sua altura em três partes iguais. Os três sólidos obtidos são: um cone de volume V1, um tronco de cone de volume V2 e um tronco de cone de volume V3, com V1 < V2 < V3.
Se V1 = K, podemos concluir que:
a) V2 = 3K e V3 = 9K
b) V2 = 8K e V3 = 27K
c) V2 = 6K e V3 = 27K
d) V2 = 7K e V3 = 19K
Resolução
Veja o que acontece quando um cone reto é dividido conforme informado pela questão:
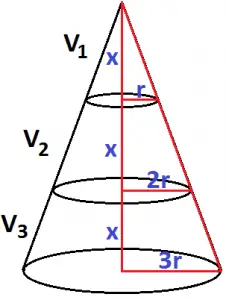
Obs: Utilizamos as regras de semelhança de triângulos para concluir que os raios medem r, 2r e 3r.
Calculando o volume do cone de altura x:
Calculando o volume do cone de altura 2x:
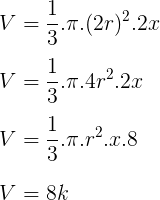
Daí,
V2 = 8k – k = 7k
Calculando o volume do cone de altura 3x:
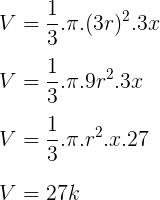
Daí,
V3 = 27k – 8k = 19k
Resposta: D
Questão 2 (EsPCEx 2010). A figura abaixo representa a planificação de um tronco de cone reto com a indicação das medidas dos raios das circunferências das bases e da geratriz.
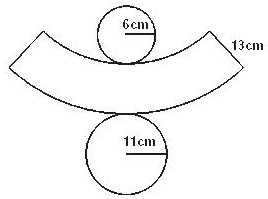A medida da altura desse tronco de cone é
a) 13 cm
b) 12 cm
c) 11 cm
d) 10 cm
e) 9 cm
Resolução
Veja na figura abaixo o tronco de cone que foi planificado.
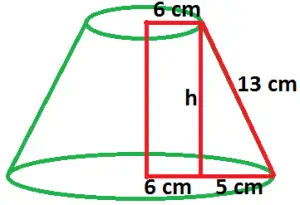
Nela é possível observar que a altura do tronco pode ser calculada através do Teorema de Pitágoras:
13² = h² + 5²
169 = h² + 25
h² = 169 – 25
h² = 144
h = √144
h = 12 cm
Resposta: B
Gostou dos nossos exercícios resolvidos sobre tronco de cone? Deixe o seu comentário.
Saber Matemática, o melhor site de matemática para concursos.