Confira aqui vários exercícios resolvidos sobre os tetraedros, todos retirados de provas de concursos públicos.
Não deixe de ver também os nossos outros conteúdos sobre geometria espacial.
Bom estudo!
Questão 1 (TJ CE – Cespe 2008). Avalie a afirmação abaixo, quanto a verdadeira ou falsa.
“O tetraedro regular é um prisma triangular cuja base corresponde a um quadrado e cujas faces são formadas por triângulos equiláteros.”
Resposta
A afirmação é falsa. O correto seria: “O tetraedro regular é uma pirâmide triangular onde todas as 4 faces são triângulos equiláteros congruentes.”
Questão 2 (FUVEST – 2013). Os vértices de um tetraedro regular são também vértices de um cubo de aresta 2. A área de uma face desse tetraedro é
a) 2√3
b) 4
c) 3√2
d) 3√3
e) 6
Resolução
A parte mais complicada da questão é “enxergar” como os vértices de um tetraedro regular podem ser vértices de um cubo. Veja como isto é possível:
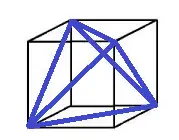
Na figura é possível observar que as arestas do tetraedro regular são diagonais das faces quadradas do cubo. Veja:
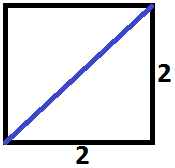
Utilizando o Teorema de Pitágoras para descobrir a medida “a” da aresta do tetraedro:
a² = 2² + 2²
a² = 4 + 4
a² = 8
a = √8
a = 2√2
Agora que sabemos a medida das arestas, basta calcular a área de uma das faces do tetraedro, ou seja, a área do triângulo equilátero de lado 2√2:
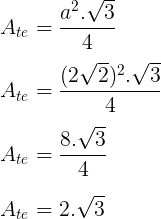
Resposta: A
