Estudando raciocínio lógico para concursos? Confira aqui vários exercícios resolvidos sobre tautologia, todos retirados das últimas seleções.

Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos do raciocínio lógico.

Bom estudo!

Questão 1 (ANVISA – CESPE 2016) . A expressão (¬P)∧((¬Q)∨R) ⇔ ¬(P∨Q) ∨ ((¬P)∧R) é uma tautologia.

a) Certo

b) Errado

Resolução

Relembrando, tautologia é uma proposição cujo valor lógico é sempre verdadeiro.

O exemplo mais trivial é a proposição p ∨ ~p que é sempre verdadeira.

A melhor forma de verificar se é uma tautologia é através da tabela verdade.

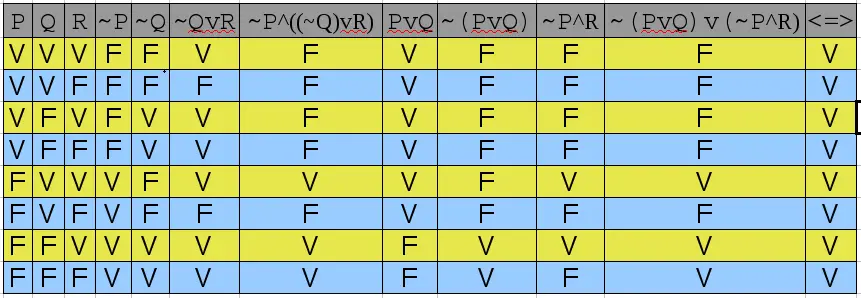
Resposta: Certo

Questão 2 (INSS 2016). Para quaisquer proposições p e q, com valores lógicos quaisquer, a condicional p ⇒ (q ⇒ p) será, sempre, uma tautologia.

a) Certo

b) Errado

Comentário

Dizemos que uma fórmula proposicional é uma tautologia quando é verdadeira para todas as opções.

Vamos então montar a tabela verdade e analisar todos os casos:

Veja que em todos os casos possíveis temos que p ⇒ (q ⇒ p) é uma verdade.

Resposta: Certo.

Questão 3 (PC ES – AOCP). Considerando p e q duas proposições quaisquer, assinale a alternativa que representa, logicamente, uma tautologia.

a) ~p ∧ p

b) ~p ∧ ~q

c) (p ∧ q) ⇒ (p ∨ q)

d) (p ∨ q) ⇒ (p ∧ q)

e) p ∨ q

Resolução

Relembrando, tautologia é uma fórmula proposicional sempre verdadeira, independentemente dos valores das proposições que a compõe.

Veja na tabela verdade abaixo que isto acontece na letra C.

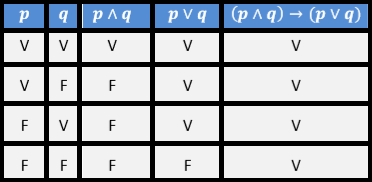
Resposta: C

Questão 4 (STJ – CESPE). A proposição ¬P⇒[P⇒Q], em que ¬P denota a negação da proposição P, é uma tautologia, isto é, todos os elementos de sua tabela-verdade são V (verdadeiro).

Resolução

Observe na tabela verdade que a proposição é sempre verdadeira.

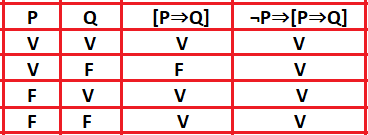
Resposta: Certo

Gostou dos nossos exercícios resolvidos sobre tautologia?

Curta e compartilhe nas redes sociais.