Procurando exercícios resolvidos sobre pirâmides? Aqui você encontra várias questões, todas retiradas dos últimos concursos públicos.
Não deixe de acompanhar também nossas outras publicações sobre geometria espacial.
Bom estudo!
Questão 1 (SISPREM RS – FUNDATEC). Um enfeite em formato de pirâmide regular e de base quadrada tem o lado da base medindo 10 cm e a altura de 30 cm. Qual é o volume em cm³ dessa pirâmide?
a) 300.
b) 690.
c) 830.
d) 950.
e) 1.000.
Resolução
Antes de calcularmos o volume da pirâmide, vamos calcular a área da base (quadrado):
Ab = 10² = 100 cm²
Calculando o volume da pirâmide:
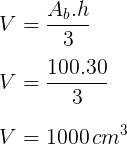
Resposta: E
Questão 2 (IBGE – FGV). Uma pirâmide regular é construída com um quadrado de 6 m de lado e quatro triângulos iguais ao da figura abaixo.
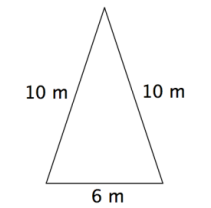
O volume dessa pirâmide em m³ é aproximadamente:
(A) 84;
(B) 90;
(C) 96;
(D) 108;
(E) 144.
Resolução:
Veja que teremos uma pirâmide onde a base é um quadrado de lado 6, e as outras 4 faces são iguais ao triângulo apresentado na figura.
Para calcularmos o volume, precisamos da área da base (6.6 = 36) e a altura da pirâmide.
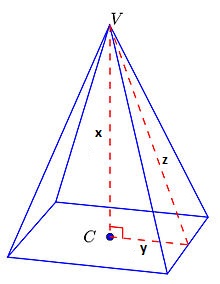
Veja na figura que nosso objetivo então será descobrir o valor de x (altura). Para tanto, precisamos saber os valores de y e z.
y é a metade do lado do quadrado, logo y=3.
z pode ser calculado utilizando o Teorema de Pitágoras no triângulo:
10² = z² + 3²
100 = z² + 9
z² = 91
z = √91
Calculando a altura x:
z² = x² + y²
(√91)² = x² + 3²
91 = x² + 9
x² = 82
x = √82 ≅ 9
Calculando o volume da pirâmide:
V = área da base x altura x 1/3
V ≅ 36.9/3
V ≅ 108 m³
Resposta: D
Questão 3 (Prefeitura de Cajamar – Moura Melo). Qual o volume de uma pirâmide regular hexagonal com 50 cm de altura e 20 cm de aresta da base?
a) 10.000 √3 cm³.
b) 3.000 √3 cm³.
c) 1.000 √3 cm³.
d) 2.400 √3 cm³.
Resolução
O volume de uma pirâmide pode ser calculado através da fórmula matemática abaixo:
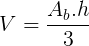
Onde:
Ab = área da base
h = altura
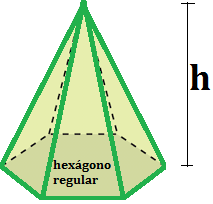
Nosso primeiro objetivo será calcular a área da base da pirâmide.
Conforme informa a questão, trata-se de um hexágono regular.
Utilizando a fórmula matemática que calcula a área de um hexágono regular:
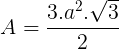
Onde:
a = lado do hexágono regular
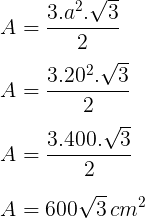
Agora que calculamos a área da base, vamos calcular o volume da pirâmide:
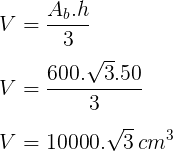
Resposta: A
Questão 4 (PM AL – CESPE). A área superficial de uma pirâmide de base quadrada regular em que todas as arestas são iguais a 2 é S = 4 + 4√3.
CERTO ou ERRADO?
Resolução
A figura abaixo apresenta uma pirâmide de base quadrada regular com as dimensões informadas.
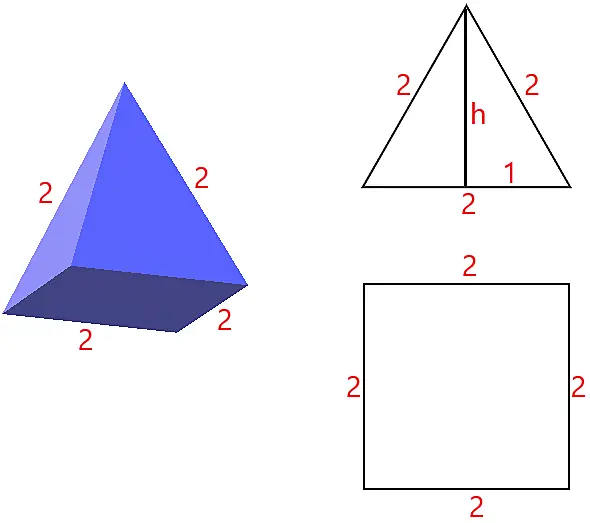
Observe que a pirâmide apresenta 4 faces de formato triangular e uma face no formato de um quadrado.
Calcularemos a altura, utilizando o Teorema de Pitágoras, e em seguida a área do triângulo.
Calculando a altura do triângulo
2² = h² + 1²
4 = h² + 1
h² = 4 – 1
h = √3
Calculando a área do triângulo
A = √3.2/2 = √3
Calculando a área do quadrado
A = 2 x 2 = 4
Consideramos que temos 4 triângulos e um quadrado, é possível calcular a área superficial da pirâmide:
4 x √3 + 4 = 4 + 4√3
Resposta: CERTO
Espero que gostem dos nossos exercícios resolvidos sobre pirâmides.
Saber Matemática, o melhor site de matemática para concursos.

A resolução da primeira questão está errada. 30 cm não é a altura da piramide porque a altura é perpendicular com a base, o que seria a apótema da piramide.
Olá Giulia!
Obrigado pela contribuição, mas o enunciado da questão informa que a altura da pirâmide mede 30 cm.
Na segunda questão fica mais fácil usar a própia aresta lateral (que vale 10m) como hipotenusa. Ficaria
100²=3²+x²; x=9. Sendo 3 metade da base.
Boa tarde, na questão 3, eu acho q houve um erro 3×20²=1200 e não 3400, logo 3400 dividido por 2 dá 1700 e não 600. Caso eu esteja errada, poderia me explicar essa questão??
Olá Luisa,
Não é 3400 e sim 3 vezes 400, que é igual a 1200, que dividido por dois, é igual a 600.