Estudando matemática para concursos? Confira aqui vários exercícios resolvidos sobre o pentágono, todos retirados das últimas provas de concursos e ENEM.
Bom estudo!
Exercício 1 (IBGE). O pentágono ABCDE tem área de 125 m2. Esse pentágono foi ampliado a partir do vértice A, como mostra a figura a seguir, transformando-se no pentágono APQRS cujos lados PQ, QR e RS são, respectivamente, paralelos aos lados BC, CD e DE do pentágono original.
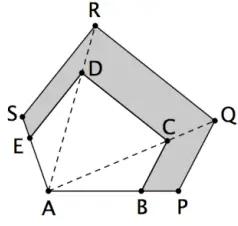
Se AB = 10 m e BP = 2 m , a área da região sombreada na figura é, em m²:
(A) 55;
(B) 64;
(C) 72;
(D) 75;
(E) 80.
Resolução:
Considerando que os polígonos são semelhantes, que x é a área do pentágono maior e que y é a área do pentágono menor, temos que:
x/y = (AP/AB)²
x/125 = (12/10)²
x/125 = 1,22
x/125 = 1,44
x = 1,44.125
x = 180m²
Portanto, a área sombreada é igual a 180 – 125 = 55 m²
Resposta: A
Exercício 2 (PM PR). Um serralheiro precisa estimar o custo de estruturas de alumínio no formato de polígonos. Essas estruturas poligonais devem ter barras diagonais para reforçá-las. O custo da estrutura metálica depende do número de barras diagonais. O número de diagonais d de um polígono de n lados é dado por uma função quadrática. Vejamos, o triângulo tem n = 3 lados e d = O diagonais, o quadrado tem n = 4 lados e d = 2 diagonais, o pentágono tem n = 5 lados e d = 5 diagonais e assim por diante. Generalizando, em um polígono de n lados, o número de diagonais d é dado por:
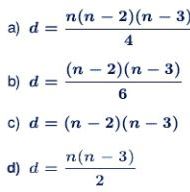
Resolução
A fórmula matemática utilizada no cálculo das diagonais de um polígono foi desenvolvida através do seguinte raciocínio:
– descontando de n os 3 vértices para onde não podem ser traçadas diagonais (os 2 adjacentes e ele mesmo): n – 3;
– multiplicando o resultado obtido pelo número de vértices: n . (n – 3);
– dividindo o resultado obtido por 2, devido às diagonais consideradas duas vezes.
Resposta: D
Exercício 3 (FGV). Um terreno tem a forma do pentágono ABCDE, como o da figura a seguir, em que os ângulos em A e B são retos e a distância AB mede 24 m. Sabe-se que o perímetro do terreno é de 84 m e que os comprimentos dos lados BC, CD, DE, e EA são todos iguais.
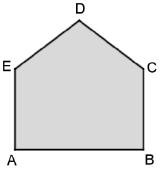
A área desse terreno, em m2, é
a) 412.
b) 440.
c) 468.
d) 480.
e) 496.
Resolução
Sabendo que AB mede 24 m, e que os lados BC, CD, DE, e EA são todos iguais, temos:
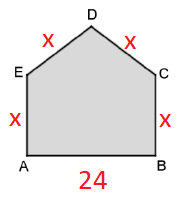
Como o perímetro mede 84 m, temos:
4x + 24 = 84
4x = 84 – 24
4x = 60
x = 60/4
x = 15 m
Como os ângulos em A e B são retos, ABCE é um retângulo de área:
24 . 15 = 360 m²
Para finalizar, precisamos calcular a área do triângulo ECD, do qual sabemos a medida da base, porém não sabemos a altura DF.
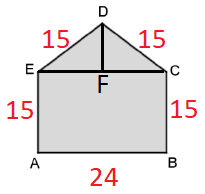
A altura de ECD pode ser calculada através do Teorema de Pitágoras, aplicado em FCD, onde FC é a metade de AB, ou seja, 12 m.
DC² = FD² + FC²
15² = FD² + 12²
225 = FD² + 144
FD² = 225 – 144
FD² = 81
FD = 9 m
Calculando a área do triângulo ECD:
24 . 9 / 2 = 12 . 9 = 108 m²
Área do pentágono:
360 + 108 = 468 m²
Resposta: C
Gostou dos nossos exercícios resolvidos sobre pentágono?
Deixe o seu comentário.
