Estudando matemática para concursos e ENEM? Confira aqui vários exercícios resolvidos sobre o Teorema de Tales.
Todas as questões foram retiradas das últimas provas de concursos.
Bom estudo!
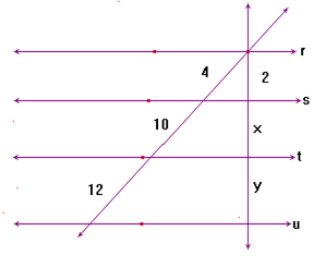
Questão 1 (IESDE – SAE – 2015). Sabendo que r // s // t // u, calcule o valor de x.
a) 5
b) 1
c) 10
d) 8
e) 6
Resolução
Sabendo que as retas r, s e t são paralelas, podemos utilizar o Teorema de Tales, onde teremos a seguinte proporção:
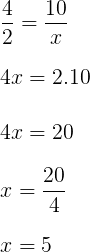
Resposta: A
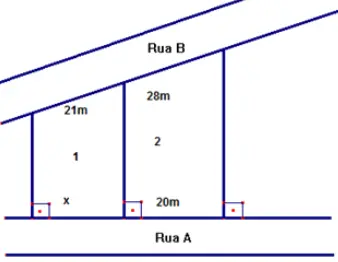
Questão 2 (IESDE – SAE – 2015). A figura abaixo indica dois lotes de terreno com frente para a rua A e para a rua B. As divisas dos lotes são perpendiculares à rua A. As frentes dos lotes 1 e 2 para a rua B medem, respectivamente, 21 m e 28 m. A frente do lote 2 para a rua A mede 20 m. Qual é a medida da frente para a rua A do lote 1?
a) 21 m.
b) 18 m.
c) 15 m.
d) 20 m.
e) 28 m.
Resolução
Como as linhas que dividem os lotes são perpendiculares à rua A, podemos concluir que são paralelas, ou seja, podemos utilizar o Teorema de Tales para resolvermos a questão.
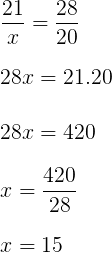
Resposta: C
Questão 3 (Inst. Machado de Assis – 2018). Utilizando a Teorema de Tales, encontre os valores de x, sabendo que as retas a, b e c são paralelas.
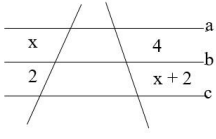
a) -2, 4
b) 2, -4
c) 2, 4
d) -1, -4
Resolução
Sabendo que as retas a, b e c são paralelas, temos a seguinte proporção:
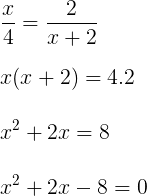
A equação do segundo grau pode ser resolvida através do método da soma e do produto, onde temos:
Soma = -b/a = -2/1 = -2
Produto = c/a = -8/1 = -8
S = {-4, 2}.
Resposta: B
Questão 4 (CEFET MG – 2014). Considere a figura em que r//s//t.
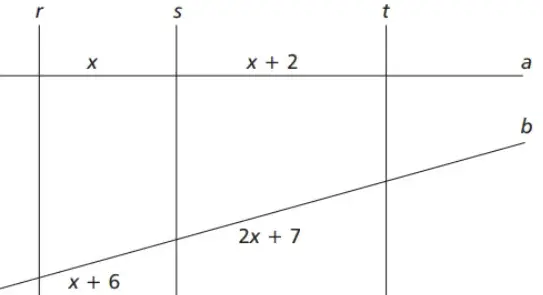
O valor de x é
a) 3.
b) 4.
c) 5.
d) 6.
Resolução
Considerando o paralelismo das retas r, s e t, temos:
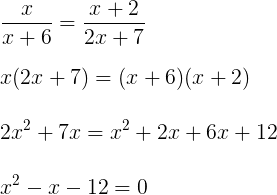
Resolvendo a equação do segundo grau através do método da soma e do produto:
Soma = -b/a = -(-1)/1 = 1
Produto = c/a = -12/1 = -12
S = {-3, 4}.
Como x representa distância, descartamos a raiz negativa.
Resposta: B
Gostou dos nossos exercícios resolvidos sobre o Teorema de Tales?
Deixe o seu comentário.
