Confira aqui vários exercícios resolvidos sobre o losango, figura muito importante da geometria plana.

Todos os exercícios foram retirados das últimas provas de concursos realizados pelo país nos últimos anos.

Bom estudo!

Questão 1 (CREA PA – FADESP 2014). Um representante do CREA de Nível Médio necessitou medir as diagonais de um terreno que tinha frente para a Rua Tocantins, media 300m² de área e possuía forma de um losango ABCD, conforme esboço abaixo.

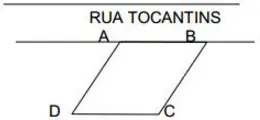
Se a diagonal maior BD era 50% maior que a diagonal menor AC, a soma dessas diagonais era igual a

a) 60 m.

b) 55 m.

c) 50 m.

d) 45 m.

Resolução

O objetivo da questão é descobrir a soma das diagonais do losango.

O enunciado nos informou a área e uma relação entre as diagonais (uma é 50% maior que a outra).

Seja x a medida da diagonal menor, de onde podemos concluir que a medida da diagonal maior será 1,5x.

Vamos agora utilizar a fórmula para o cálculo da área do losango:

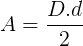
300 = 1,5x.x/2

1,5x² = 300.2

1,5x² = 600

x² = 600/1,5

x² = 400

x = √400

x = 20 m

Logo, as diagonais são 20 e 30 metros.

20 + 30 = 50 metros

Resposta: C

Questão 2 (PM Natal – Consulplan 2013). Observe o losango. A medida do ângulo x é igual a

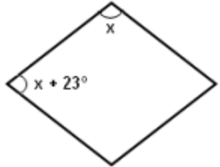
A) 66°.

B) 74,2°

C) 78,5°.

D) 87°.

Resolução

Sabe-se que a soma de dois ângulos adjacentes de um losango mede 180º.

x + x + 23º = 180º

2x = 180º – 23º

2x = 157º

x = 157º/2

x = 78,5º

Resposta: C

Questão 3 (Pref. de Coroados SP – Excelência 2018). Calcule a área da figura a seguir:

D= 9.

d= 2.

Assinale a alternativa CORRETA.

a) 11

b) 18

c) 9

d) Nenhuma das alternativas

Resolução

A questão apresenta a figura de um losango, onde são dadas as medidas das diagonais.

Utilizando a fórmula da área do losango, temos:

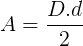
A = 9.2/2

A = 9

Resposta: C

Questão 4 (Objetiva Concursos). Considerando-se um losango, que possui 80cm² de área, assinalar a alternativa que apresenta uma possível medida para a sua diagonal maior e para a sua diagonal menor, respectivamente:

A) 10cm e 8cm

B) 12cm e 10cm

C) 14cm e 8cm

D) 16cm e 10cm.

E) 16cm e 5cm.

Resolução

Utilizaremos a fórmula da área de um losango, considerando que o losango em questão possui área igual a 80 cm².

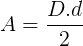
80 = D.d/2

D.d = 80.2

D.d = 160

Observe que o produto das duas diagonais deve ser igual a 160, e a única alternativa com essa característica é a alternativa D.

16 x 10 = 160

Resposta: D

Questão 5 (Vunesp – Oficial da PM SP). Em uma circunferência de raio x cm e centro O, considere uma reta t tangente em um ponto C e a corda AB paralela à reta t, corda essa que é a diagonal maior do losango AOBC, conforme mostra a figura.

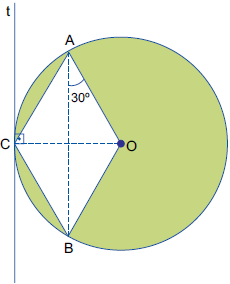
Se AB=12√3​ cm, então a área destacada em verde mede, em cm²,

A) 723

​B) 72(π − √3​)

C) 72(2π − √3​)

D) 48(2π − √3​)

E) 48(π − √3​)

Resolução

Observe que a área destacada em verde é a diferença entre a área da circunferência e a área do losango. Calcularemos a área das duas figuras e depois a diferença entre elas.

Considerando que AB = 12√3 cm, e que cada diagonal de um losango divide a outra em duas partes iguais, podemos utilizar as seguintes medidas, onde consideramos o raio da circunferência igual a x.

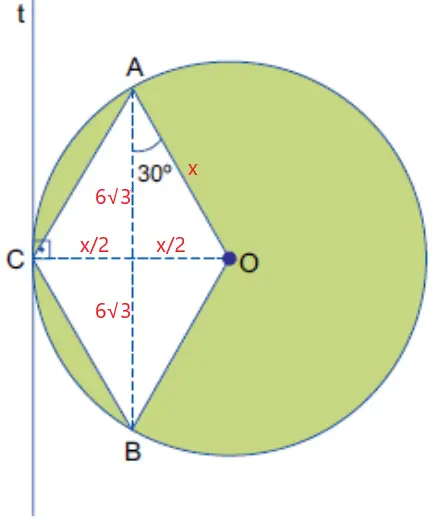
Considerando que cos30º = √3/2 e que a figura formada pelos pontos A, O e pelo centro do losango é um triângulo retângulo, podemos utilizar a seguinte relação:

cos30º = 6√3 / x

√3/2 = 6√3 / x

x = 12

Área da circunferência

A = π.r²

A = π.12²

A = π.144

A = 144π

Área do losango

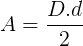
A = 12√3 . 12 / 2

A = 72√3

Área destacada em verde

144π – 72√3 = 72(2π – √3)

Resposta: C

Gostou dos nossos exercícios resolvidos sobre losango?

Deixe o seu comentário.