Estudando matemática para concursos? Confira aqui vários exercícios resolvidos sobre a cônica hipérbole, todos retirados dos últimos concursos públicos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria analítica.
Bom estudo!
Questão 1 (Petrobrás – Cesgranrio 2010). Os vértices imaginários da hipérbole de equação abaixo são:
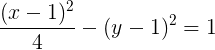
a) (2,1) e (2,3)
b) (2,0) e (2,2)
c) (2,0) e (1,2)
d) (1,1) e (1,2)
e) (1,0) e (1,2)
Resolução
O primeiro passo é identificar as informações contidas na equação da hipérbole:
O centro é (1,1)
a = 2 e b = 1
Com as informações acima, podemos desenhar a seguinte hipérbole:
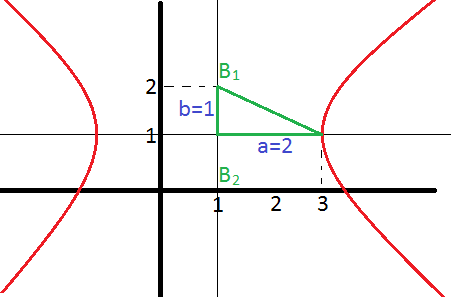
Nele é possível observar que os eixos imaginários B1 e B2 são, respectivamente, (1,2) e (1,0).
Resposta: E
Questão 2 (IDECAN). Dados dois pares ordenados (2,-4) e (2,0) que representam os vértices de um hipérbole de foco (2, -2 + √13), calcule a equação da hipérbole que satisfaça as condições dadas.
a) 4x2 – 9y2 – 16x – 36y +16 = 0
b) 2x2 – 3y2 – 16x – 36y + 16 = 0
c) 4x2 – 9y2 + 16x – 36y – 16 = 0
d) 4x2 − 5y2 − 16x – 36y + 16 = 0
e) 4x2 – 16x – 36y + 16 = 0
Resolução
Localizando os vértices (2,0) e (2,-4), e o foco (2, -2 + √13), é possível fazer um esboço da hipérbole:
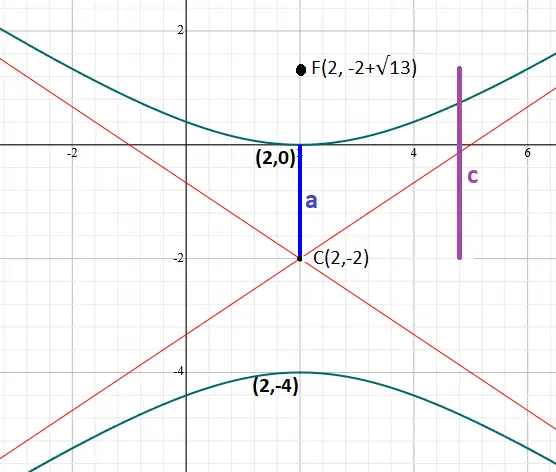
A equação geral de uma hipérbole deste tipo é:
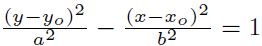
Onde (x0,y0) é o centro e as medidas “a” e “b” representam metade dos eixos real e imaginário, respectivamente.
Na imagem é possível observar que o centro da hipérbole é o ponto (2,-2), a=2, e que:
c = -2 + √13 + 2 = √13
Em toda hipérbole vale a seguinte relação:
c² = a² + b²
√13² = 2² + a²
13 = 4 + a²
a² = 13 – 4
a² = 9
a = √9
a = 3
Voltando a equação geral:
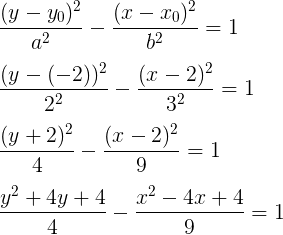
Multiplicando a equação por 36 e simplificando, temos:
4x2 – 9y2 – 16x – 36y +16 = 0
Resposta: A
Gostou dos nossos exercícios resolvidos sobre a hipérbole?
Deixe o seu comentário.
