Confira aqui vários exercícios resolvidos sobre funções monótonas, todos retirados de provas de concursos, vestibulares e ENEM.
Bom estudo!
Questão 1 (UP). Quais são os intervalos de monotonia da função
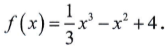
a) f(x) cresce para x∈]-∞, 2[ e decresce para x∈]2, +∞[
b) f(x) cresce para x∈]-∞, 0[ e decresce para x∈]0, +∞[
c) f(x) cresce para x∈]0, 2[ e decresce para x∈]-∞, 0[∪]2, +∞[
d) f(x) cresce para x∈]-∞, 0[∪]2, +∞[ e decresce para x∈]0, 2[
Resolução
A forma mais fácil de verificarmos os intervalos de monotonia de uma função é através da derivação.
Quando a função derivada é positiva, a função é crescente, e quando a função derivada é negativa, a função é decrescente.
f'(x) = x² – 2x
Veja que a derivada é uma função do segundo grau.
Calculando as raízes:
x² – 2x = 0
x(x – 2) = 0
As raízes são 0 e 2.
Como o gráfico de uma função quadrática possui o formato de uma parábola, a>0, e as raízes são 0 e 2, ele terá o seguinte formato:
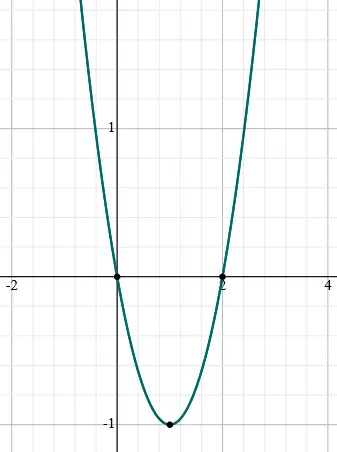
Daí, a função f será crescente para x < 0 ou x > 2, e decrescente para 0 < x < 2.
Resposta: D
Gostou dos nossos exercícios resolvidos sobre funções monótonas?
Deixe o seu comentário.
