Confira nesta página uma seleção especial de exercícios resolvidos sobre a função inversa. Todos foram retirados de questões presentes nas últimas provas de concursos públicos.

Lembrando que o ideal é que você tenha lido os conteúdos sobre a definição de funções e sobre a função inversa.

Bons estudos!

Questão 1 (SEDUC RJ). Considere a função de variável real f(x) = (3x + 8)/2. Qual o valor de f^-1(10)?
a) 1 ⁄ 19

b) 6

c) 0,25

d) 4

e) 19

Resolução

Na função f temos que:

y = (3x + 8)/2

Para descobrirmos a regra da função inversa, devemos colocar x em função de y:

y = (3x + 8)/2

2y = 3x + 8

2y – 8 = 3x

x = (2y – 8)/3

Trocando x por y, temos que:

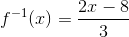
Basta agora calcularmos o valor da inversa quando x = 10:

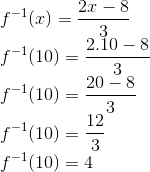
Resposta: D

Questão 2 (EEAR) Seja a função f : R → R definida por f(x) = 4x – 3. Se f^-1 é a função inversa de f, então f^-1(5) é

a) 17

b) 1/17

c) 2

d) 1/2

Resolução

A regra de f é dada por y = 4x – 3

Vamos calcular a sua função inversa:

y = 4x – 3

y + 3 = 4x

x = (y + 3)/4

Invertendo x e y, temos:

f^-1(x) = (x + 3)/4

f^-1(5) = (5 + 3)/4 = 8/4 = 2

Resposta: C

Questão 3 (RFB). A função bijetora dada por f(x) = (x+1)/(x-2) possui domínio no conjunto dos números reais, exceto o número 2, ou seja: R – {2}. O conjunto imagem de f(x) é o conjunto dos reais menos o número 1, ou seja: R – {1}. Desse modo, diz-se que f(x) é uma função de R – {2} em R – {1}. Com isso, a função inversa de f, denotada por f^-1 , é definida como

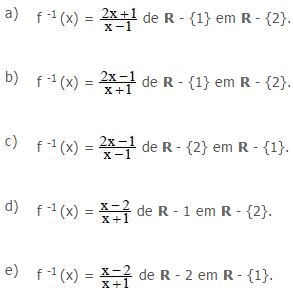
Resolução

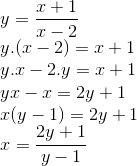
Invertendo x e y, temos a função inversa:

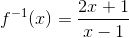
Quanto ao domínio e a imagem, a função será de de R – {1} em R – {2}. Como trata-se de uma função bijetora e inversível, basta invertermos.

Resposta: A

Questão 4 (UP). Sendo f(x) = log₃(x+1) – 2 uma função de ]-1, +∞[ →R, qual é a sua função inversa?

a) f^-1(x) = 3^x-2 + 1

b) f^-1(x) = 3^x-2 – 1

c) f^-1(x) = 3^x+2 – 1

d) f^-1(x) = 3^x+2 + 1

Resolução

Considerando a função, com f(x) = y, temos:

log₃(x+1) – 2 = y

log₃(x+1) = y + 2

Pela definição de logaritmos:

3^{(y + 2)} = x + 1

3^{(y + 2)} – 1 = x

x = 3^{(y + 2)} – 1

Invertendo as variáveis:

f^-1(x) = 3^x+2 – 1

Resposta: C

Gostou dos nossos exercícios resolvidos sobre função inversa?

Deixe o seu comentário.