Confira aqui vários exercícios resolvidos sobre estatística, onde abordaremos os mais variados assuntos relacionados ao conteúdo.
Lembrando que todas as questões foram retiradas de provas de concursos.
Bom estudo!
Questão 1 (PM MG). O Comandante da 500ª CIA PM promoveu um torneio operacional, de forma que os militares da CIA PM foram divididos em 04 equipes para realizarem 03 provas distintas, no valor de 10 pontos cada uma, com os seguintes temas: técnica policial-militar, abordagem a veículos e controle de distúrbios. As provas teriam pesos 3, 2 e 1, respectivamente.
TABELA: notas das provas da gincana da 500ª CIA PM, por equipe e tema:
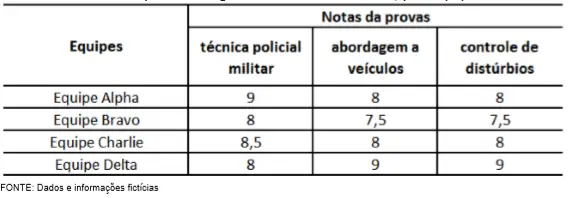
Considerando a média ponderada de cada equipe, marque a alternativa CORRETA.
A. ( ) A Equipe Alpha obteve média ponderada inferior à Equipe Charlie.
B. ( ) A Equipe Bravo obteve média ponderada de 8,25.
C. ( ) A Equipe Delta obteve a mesma média ponderada que a equipe Alpha.
D. ( ) A Equipe Charlie obteve média ponderada superior à Equipe Delta.
Resolução
Calculando a média ponderada de cada uma das equipes:
Equipe Alpha
(3.9 + 2.8 + 1.8) / 6 = 8,5
Equipe Bravo
(3.8 + 2.7,5 + 1.7,5) / 6 = 7,75
Equipe Charlie
(3.8,5 + 2.8 + 1.8) / 6 = 8,25
Equipe Delta
(3.8 + 2.9 + 1.9) / 6 = 8,5
Resposta: C
Questão 2 (CESPE – Correios). Uma cadeia de Markov é denominada irredutível (ou ergódica) caso qualquer estado possa ser transformado em qualquer outro estado, não necessariamente em um único passo. Uma cadeia de Markov com matriz de transição P é regular caso exista um número inteiro positivo n tal que todos os elementos da matriz potência Pn sejam estritamente positivos.
Julgue o seguinte item a respeito desses conceitos.
“O dígrafo abaixo representa uma cadeia de Markov regular.”

Resolução
O dígrafo pode ser representado pela seguinte matriz de transição:

Tem dúvidas acerca da formação da matriz de transição?
Note que o elemento p23 é igual a probabilidade de chegar em 3, saindo de 2.
Por definição, uma cadeia de Markov é regular se existe um natural r0 tal que para todo r≥r0, (pij)r > 0, ∀i,j∈S. Ou seja, se existe uma potência de P com todas as entradas positivas.
Observe que para qualquer valor de n, Pn terá todos os elementos maiores que zero, ou seja, matriz regular.
Resposta: Certo
Questão 3 (SEFAZ PI – FCC). O número de falhas mensais de um computador é uma variável que tem distribuição de Poisson com média λ. Sabe-se que λ é igual à média de uma distribuição uniforme no intervalo [2, 4]. Nessas condições, a probabilidade de o computador apresentar exatamente duas falhas no período de 15 dias é igual a:
Dados: e-3 = 0,05; e-1,5 = 0,22.
a) 22,50%
b) 12,50%
c) 24,15%
d) 15,25%
e) 24,75%
Resolução
A média de uma distribuição uniforme no intervalo [a, b] é a média aritmética dos valores a e b. Assim, a média da distribuição uniforme no intervalo [2, 4] é dada por:
(2 + 4)/2 = 3
Veja que o valor encontrado corresponde ao período de um mês, ou seja, a média de falhas a cada 15 dias é igual a 1,5.
Como a questão pede a probabilidade do computador apresentar exatamente duas falhas no período de 15 dias, utilizaremos a fórmula da distribuição de Poisson, onde λ=1,5 e X=2:
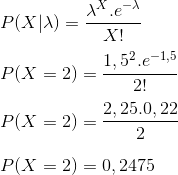
Resposta: E
Questão 4 (TRE PI – FCC). O diagrama de ramo e folhas abaixo corresponde às observações das idades de 50 eleitores escolhidos aleatoriamente em uma determinada zona eleitoral:

O valor do módulo da diferença entre a mediana e a moda destas idades observadas é
A) 0
B) 3
C) 10
D) 14
E) 16
Resolução
Temos um diagrama de ramos e folhas que representa a idade de 50 pessoas.
Dispostas em ordem crescente, a mediana das idades é a média dos 25º e 26º termos:
(32 + 32) / 2 = 32
A moda é a idade que aparece com maior frequência. Temos 4 eleitores com 46 anos.
Calculando o módulo da diferença (o maior pelo menor):
46 – 32 = 14
Resposta: D
Questão 5 (TSE). Para uma população de 10 indivíduos é retirada uma amostra de 3 indivíduos, sem reposição. Assim, o número de amostras possíveis é
a) 80.
b) 120.
c) 240.
d) 720.
Resolução
A questão informa o tamanho da população (10 pessoas) e o tamanho da amostra (3 pessoas).
Como precisamos calcular a quantidade de amostras possíveis, basta calcularmos a quantidade de combinações de 10 pessoas, tomadas 3 a 3.
C3,3 = 10! / 7!.3! = 10.9.8/3.2.1 = 120
Resposta: B
Questão 6 (SUDAM AM – IADES). Em 20 dias de aula, um professor de estatística anotou o número de alunos ausentes. Depois, fez a seguinte tabela de frequências:
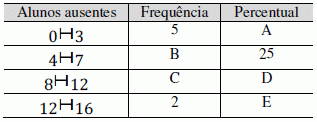
A letra B representa o número
A) 5.
B) 6.
C) 7.
D) 8.
E) 9.
Resolução
Analisando a segunda classe, temos que B representa 25% da quantidade de dias de aula.
Como o professor fez a pesquisa durante 20 dias, temos que B = 5.
Resposta: A
Gostou dos nossos exercícios resolvidos sobre estatística?
Deixe o seu comentário.
