Confira aqui vários exercícios resolvidos sobre esfera, todos retirados dos últimos concursos públicos realizados pelo Brasil.

Não deixe de ver também nossos exercícios resolvidos sobre os outros sólidos geométricos.

Bom estudo!

Questão 1 (CEMIG). O volume de uma esfera de raio r é (4/3).π.r³. Se um balão esférico é inflado até que o seu raio seja quadruplicado, então o seu volume é aumentado pelo fator:

a) 1024

b) 256

c) 64

d) 164

Resolução

Nota-se que a fórmula matemática utilizada para o cálculo do volume de uma esfera está em função apenas de r.

Como o raio será quadruplicado, veja o que vai acontecer quando elevamos ao cubo:

(4r)³ = 4³.r³ = 64.r³

Daí, quando o raio de uma esfera é quadruplicado, o volume passa a ser 64 vezes maior que o inicial.

Resposta: C

Questão 2 (FCC). Uma pessoa fez quatro cortes paralelos igualmente espaçados em uma laranja esférica, dividindo-a nas cinco partes indicadas na figura.

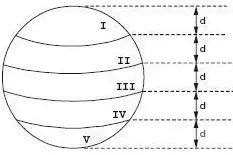
Em relação a essa divisão, é correto afirmar que

a) todas as partes obtidas têm o mesmo volume.

b) a parte III é a de maior volume.

c) o volume da parte I é maior do que o volume da parte II.

d) não foram obtidas duas partes com o mesmo volume.

e) a soma dos volumes das partes IV e V é menor do que a soma dos volumes das partes I e II.

Resolução

Como os cortes foram paralelos e igualmente espaçados, a parte que possuirá o maior volume será a que possui o maior raio. Nesta caso, a região de maior volume é a III.

Resposta: B

Questão 3 (AMEOSC). Pretende-se encher uma bexiga até que ela atinja 20 cm de diâmetro. Considere que essa bexiga é esférica. Quantos litros de água serão necessários?

a) 4,2 litros.

b) 3,8 litros.

c) 3,1 litros.

d) 2,5 litros.

Resolução

Para resolvermos a questão, é necessário sabermos que um litro de água enche uma esfera de volume igual a 1 dm³.

Desta forma, consideraremos que o diâmetro deve atingir 2 dm, e o raio 1 dm.

Calculando o volume da esfera:

V = (4/3) . π . r³

V = (4/3) . 3,14 . 1³

V = (4/3) . 3,14 . 1

V = 4,19 dm³

Daí, são necessários, aproximadamente 4,2 litros.

Resposta: A

Questão 4 (Funcab). O único sólido geométrico que NÃO pode ser planificado é o(a):

a) paralelepípedo

b) pirâmide

c) esfera

d) cilindro

e) cone

Resolução

Em nossas publicações, vimos que o paralelepípedo, a pirâmide, o cilindro e o cone podem ser planificados. O único sólido dentre as opções que não pode ser planificado é a esfera. Um exercício interessante que o aluno pode fazer caso tenha dúvida, é descascar uma laranja e tentar colocar todas as cascas no plano.

Resposta: C

Exercício 5 (Funcab). No ensino de geometria, nas séries iniciais, tem sua importância social o reconhecimento do universo tridimensional. Pensando nisso, uma professora levou para uma de suas aulas os objetos abaixo:

I. Uma caixa de sapato (paralelepípedo).

II. Uma lata de leite em pó (cilindro).

III. Uma bola de futebol (esfera).

Os sólidos acima são, respectivamente:

a) poliedro, sólido de revolução e poliedro.

b) sólido de revolução, poliedro e poliedro.

c) sólido de revolução, sólido de revolução e poliedro.

d) poliedro, sólido de revolução e sólido de revolução.

e) sólido de revolução, sólido de revolução e sólido de revolução.

Resolução

I – o paralelepípedo é um tipo de poliedro, que é um sólido geométrico de três dimensões, cuja superfície é formada por um número finito de superfícies planas.

II – um cilindro reto é um sólido de revolução, gerado pela rotação de um retângulo em torno de um de seus lados.

III – uma esfera é um sólido de revolução gerado pela rotação de um semicírculo em torno de um eixo que contém o diâmetro.

Resposta: D

Exercício 6 (IGETEC). O hexaedro regular que inscreve a esfera de volume 9π/2 cm³, tem a medida da diagonal, em centímetros, igual a:

a) 2,7

b) √3

c) 3√3

d) 3

Resolução

O hexaedro regular é o objeto que conhecemos como cubo.

Quando a questão informa que o cubo “inscreve a esfera”, ela quer dizer que a esfera está dentro do cubo. Desta forma, se o raio da circunferência mede r, cada aresta do cubo medirá 2r. Veja:

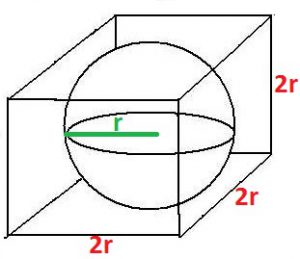
Como sabemos o volume da esfera, vamos utilizar a fórmula do volume para calcularmos a medida do raio r.

V = (4/3).π.r³

9π/2 = (4/3).π.r³

9/2 = (4/3).r³

r³.(4/3) = 9/2

r³ = (9/2).(3/4)

r³ = 27/8

r = 3/2 cm

Daí, concluímos que o raio mede 3/2 cm e as arestas do cubo medem 3 cm.

Utilizando a fórmula matemática que calcula a diagonal do cubo:

D = a.√3

D = 3.√3

Resposta: C

Gostou dos nossos exercícios resolvidos sobre a esfera?

Deixe o seu comentário.