Estudando matemática para concursos? Confira aqui vários exercícios resolvidos sobre o cálculo da distância entre ponto e circunferência.

Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria analítica.

Bom estudo!

 

 

Questão 1. Calcule a distância entre o ponto P(-3, -2) e a circunferência x² + (y – 2)² = 16.

 

Resolução

Analisando a equação reduzida da circunferência, temos que o centro é C(0, 2) e o raio é 4.

 

Calculando a distância entre o ponto P e o centro C:

d² = (-3 – 0)² + (-2 – 2)²

d² = 3² + 4²

d² = 9 + 16

d² = 25

d = √25

d = 5

 

Como a distância entre C e P é igual a 5 e o raio da circunferência é igual a 4, podemos concluir que o ponto é exterior à circunferência e a distância entre ambos é de:

5 – 4 = 1.

 

 

Questão 2. Calcule a distância entre o ponto P(1, 1) e a circunferência (x – 2)² + (y – 3)² = 49.

 

Resolução

Analisando a equação reduzida da circunferência, temos que o centro é C(2, 3) e o raio é igual a 7.

 

Calculando a distância entre o ponto P e o centro C:

d² = (2 – 1)² + (3 – 1)²

d² = 1² + 2²

d² = 1 + 4

d² = 5

d = √5

 

Como √5 < 7, podemos concluir que o ponto é interior à circunferência e a distância entre eles é de 7 – √5.

 

 

Questão 3. Seja o ponto P(2, k) e a circunferência (x – 3)² + (y – 1)² = 64. Calcule o valor de k que faz com que P pertença à circunferência.

 

Resolução

A equação reduzida nos informa que o raio é 8 e o centro é C(3, 1).

 

Calculando a distância entre o centro e o ponto P:

d² = (3 – 2)² + (1 – k)²

 

Como o ponto pertence à circunferência quando a distância até o centro é igual ao raio, podemos considerar d = r = 8.

8² = 1² + 1² – 2k + k²

64 = 2 – 2k + k²

k² – 2k – 62 = 0

 

Δ = b² – 4.a.c

Δ = (-2)² – 4.1.(-62)

Δ = 4 + 248

Δ =252

 

 

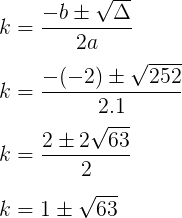
Daí, existem dois valores para k que fazem com que o ponto P pertença à circunferência:

k = 1 + √63

k = 1 – √63

 

 

Gostou dos nossos exercícios resolvidos sobre a distância entre ponto e circunferência?

Deixe o seu comentário.