Confira aqui vários exercícios resolvidos sobre disjunção exclusiva, todos retirados das últimas provas de concursos.
Veja também em nosso menu vários outros exercícios resolvidos sobre os diversos tópicos do raciocínio lógico matemático.
Bom estudo!
Questão 1 (PERPRO – Quadrix). A tabela a seguir é a tabela verdade para duas proposições simples a e b, considerando-se o Conectivo do tipo DISJUNÇÃO EXCLUSIVA.
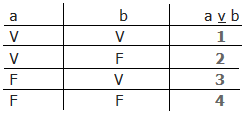
Assinale a alternativa que contém os valores corretos para 1, 2, 3 e 4.
a) 1- F, 2–F, 3-F, 4-F
b) 1-F, 2-V, 3-V, 4-F
c) 1-V, 2-F, 3-V, 4-V
d) 1-V, 2- F, 3-F,4-F
e) 1-V ,2 -V, 3-V, 4-V
Resolução
A disjunção exclusiva é verdadeira apenas quando apenas uma das proposições envolvidas assume valor verdadeiro.
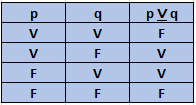
Resposta: B
Questão 2 (PM ES – AOCP). Em um teste de aptidão física de dois soldados, X e Y, um sargento afirmou aos seus superiores que “ou o soldado X foi aprovado ou o soldado Y foi reprovado”.
A negação dessa afirmação é
(A) “O soldado X foi reprovado e o soldado Y foi reprovado”.
(B) “O soldado X foi aprovado ou o soldado Y foi aprovado”.
(C) “O soldado X foi aprovado e o soldado Y foi aprovado”.
(D) “O soldado X foi aprovado se e somente se o soldado Y foi reprovado”.
(E) “Se o soldado X foi reprovado, então o soldado Y foi reprovado”.
Considere:
p: o soldado X foi aprovado
q: o soldado Y foi reprovado
Podemos representar a disjunção exclusiva “ou o soldado X foi aprovado ou o soldado Y foi reprovado” da seguinte forma:
p ⊕ q
Utilizando as equivalências lógicas:
~(p ⊕ q) = p⇔q
Finalizando,
p⇔q: o soldado X foi aprovado se e somente se o soldado Y foi reprovado
Resposta: D
Questão 3 (Petrobras – Cesgranrio). A disjunção exclusiva, denotada por ⊕, é uma operação lógica que assume valor verdadeiro quando, e somente quando, apenas uma das proposições envolvidas assumir valor lógico verdadeiro.
Considere as proposições:
p: A equipe x participa do campeonato.
q: A equipe y fica na 2a colocação do campeonato.
Por qual proposição a negação de p ⊕ q pode ser expressa?
a) Se a equipe x participa do campeonato, então a equipe y fica na 2a colocação do campeonato.
b) A equipe x participa do campeonato ou a equipe y fica na 2a colocação do campeonato.
c) A equipe x participa do campeonato e a equipe y fica na segunda colocação do campeonato.
d) A equipe x não participa do campeonato e a equipe y não fica na 2a colocação do campeonato.
e) A equipe y fica na segunda colocação do campeonato se e somente se a equipe x participa do campeonato.
Resolução
Basta analisar as tabelas verdade para concluirmos que a negação da disjunção exclusiva é o bicondicional.
~(p ⊕ q) = p ⇔ q

![]()
Resposta: E
Gostou dos nossos exercícios resolvidos sobre disjunção exclusiva?
Deixe o seu comentário.
