Confira aqui vários exercícios resolvidos sobre cone, todos retirados das últimas provas de concursos.

Não deixe de ver também nossos exercícios resolvidos sobre outros sólidos geométricos e também sobre a geometria espacial.

Bom estudo!

Questão 1 (PM ES – Exatus 2013). O volume do sólido gerado pela rotação de um triângulo isósceles de lados congruentes medindo 5 cm e base medindo 6 cm, em torno da base é igual a:

a) 32π cm³

b) 13π cm³

c) 14π cm³

d) 15π cm³

e) 16π cm³

Resolução

Veja na figura abaixo que, após a rotação em torno da base do triângulo isósceles, teremos um sólido formado por dois cones iguais.

Calcularemos o volume de um deles, e depois multiplicaremos por 2.

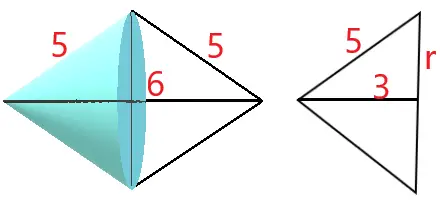
Utilizaremos o Teorema de Pitágoras para o cálculo do raio da base do cone:

5² = 3² + r²

25 = 9 + r²

r² = 25 – 9

r² = 16

r = √16

Calculando o volume do cone:

V = Área da base x altura / 3

V = π . 4² . 3 / 3

V = π . 16

V = 16π cm³

Volume total:

2 . 16π = 32π cm³

Resposta: A

Questão 2 (PM ES – Exatus 2013). Dados um cilindro circular reto e um cone circular reto de mesma altura e mesmo raio, é correto afirmar que o volume do cone é igual a:

a) três vezes o volume do cilindro

b) duas vezes o volume do cilindro

c) metade do volume do cilindro

d) terça parte do volume do cilindro

e) sexta parte do volume do cilindro

Resolução:

Vamos comparar cada uma das fórmulas utilizadas para o cálculo do volume do cone e do cilindro.

Fórmula para cálculo de volume de cilindros:

V = π.r².h

Fórmula para cálculo de volume de cones:

V = (π.r².h)/3

Como altura e raio são iguais, claramente o volume do cone é 1/3 do volume do cilindro.

Resposta: D

Questão 3 (SEDUC RJ – COPERJ 2011). A figura abaixo mostra um cilindro reto inscrito em um cone: a base inferior do cilindro está sobre a base do cone, e a circunferência da base superior do cilindro está sobre a superfície lateral do cone.

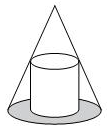
Sabe-se que a altura do cilindro é a metade da altura do cone e que o volume do cilindro é de 150 cm³ . O volume do cone é:

a) 400 cm³

b) 360 cm³

c) 300 cm³

d) 240 cm³

e) 200 cm³

Resolução

Veja na figura abaixo que podemos utilizar a semelhança de triângulos para concluir que o raio do cilindro também é metade do raio do cone.

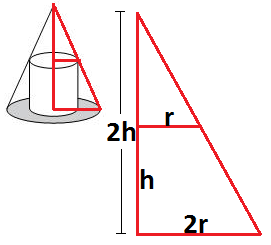
Volume do cilindro

V_ci = área da base . altura

150 = π.r².h

Volume do cone

V_co = área da base . altura / 3

V_co = π.(2r)².2h/3

V_co = π.4r².2h/3

V_co = 8π.r².h/3

Como π.r².h = 150, temos:

V_co = 8.150/3

V_co = 400 cm³

Resposta: A

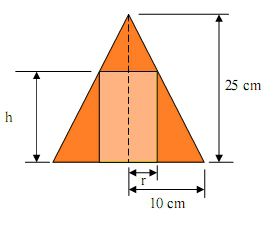
Questão 4 (PRF 2008). Considere que um cilindro circular reto seja inscrito em um cone circular reto de raio da base igual a 10 centímetros e a altura igual a 25 centímetros, de forma que a base do cilindro esteja no mesmo plano da base do cone. Em face dessas informações e, considerando, ainda, que h e r correspondam à altura e ao raio da base do cilindro, respectivamente, assinale a opção correta.

a) A função afim que descreve h como função de r é crescente.

b) O volume do cilindro como uma função de r é uma função quadrática.

c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50.π.r (1 – r/10)

d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.

e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.

Resolução

Veja na figura que o cilindro está dentro do cone.

• 

Analisando cada uma das alternativas.

a) A função afim que descreve h como função de r é crescente.

Basta verificar que a medida que r aumenta, h diminui, ou seja, a função é decrescente.

Para encontrar a equação de h, vamos usar o método dos triângulos proporcionais. Se o triângulo maior, ABC, e o triângulo menor CDE. Veja:

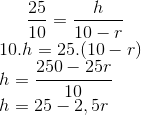
Obs: o fato de -2,5r ser negativo nos prova que a função afim é decrescente.

b) O volume do cilindro como uma função de r é uma função quadrática.

Utilizando a fórmula:

V = π.r².h

V = π.r².(25 – 25r/10)

V = 25π.r² – 25π.r³/10

Veja que a função é cúbica e não quadrática.

c) Se A(r) é a área lateral do cilindro em função de r, então A(r) = 50 r.

A(r) = base.altura = 2π.r.h = 2π.r.(25 – 25r/10) = 50π.r (1 – r/10)

d) É possível encontrar um cilindro de raio da base igual a 2 centímetros e altura igual a 19 centímetros que esteja inscrito no referido cone.

h = 25 – 25r/10 = 25 – 25.2/10 = 25 – 5 = 20

e) O cilindro de maior área lateral que pode ser inscrito no referido cone tem raio da base superior a 6 centímetros.

A(r) = 50π.r (1 – r/10) = 50π.r – 5π.r². (função quadrática decrescente, o ponto máximo de r é o vértice)

xv = -b/2a – -50π/2(-5π) = 5

Resposta: C

Gostou dos nossos exercícios resolvidos sobre o cone? Deixe o seu comentário.

Saber Matemática, o melhor site de matemática para concursos.