Confira aqui vários exercícios resolvidos sobre o cálculo da probabilidade da união de dois eventos, todos retirados dos últimos concursos públicos.

Não deixe de ler primeiro o nosso conteúdo sobre o assunto.

Bom estudo!

 

 

Questão 1 (Prefeitura de Porto Alegre – Fundatec 2012). Uma questão de uma prova de Estatística apresenta grau médio de dificuldade. João tem 75% de chance de resolvê-la, e Daniel tem 60% de probabilidade de não resolvê-la. Se eles tentam resolver a questão de modo independente, qual será a probabilidade de que a questão seja resolvida?

A) 22,5%

B) 55,0%

C) 70,0%

D) 75,5%

E) 85,0%

 

Resolução

Sejam os eventos:

A: João conseguir resolver a questão

B: Daniel conseguir resolver a questão

 

Pelo enunciado temos:

P(A) = 75%

P(B) = 40%

P(A∩B) = 75% x 40% = 30%

 

Utilizando a fórmula matemática que calcula a probabilidade da união de dois eventos:

P(A ∪ B) = P(A) + P(B) – P (A ∩ B )

P(A ∪ B) = 75% + 40% – 30%

P(A ∪ B) = 85%

 

Resposta: E

 

 

Questão 2 (TJ BA – FGV 2015). A probabilidade da união de dois eventos, A e B, é conhecida, sendo igual a 80%, enquanto a probabilidade da união de seus complementares é igual a 70%. Assim, se a probabilidade de A é igual a 40%, então:

a) P(B) = 0,70;

b) P(B) = 0,25.

c) P(B) = 0,30;

d) P(B) = 0,50;

e) P(B) = 0,60.

 

Resolução

Vamos resolver o exercício utilizando a fórmula matemática abaixo (probabilidade da união de dois eventos):

P (A ∪ B) = P(A) + P(B) – P(A ∩ B)

 

Onde:

P (A ∪ B) = 0,8 ou 80% (informação retirada do enunciado)

P(A) = 0,4 ou 40% (informação retirada do enunciado)

P(A ∩ B) = 0,3 ou 30%

 

O valor de P(A ∩ B) foi retirado da informação “a probabilidade da união de seus complementares é igual a 70%”. Veja os diagramas abaixo:

Complementar do conjunto A

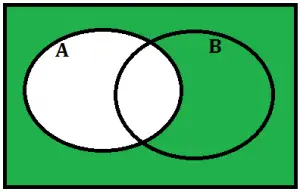
Complementar do conjunto B

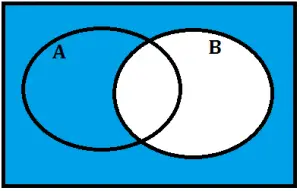
União dos complementares de A e B

 

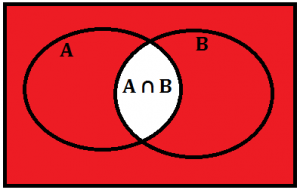
Temos que:

P(A ∩ B) = 1 – P(A^c ∪ B^c )

P(A ∩ B) = 1 – 0,7

P(A ∩ B) = 0,3 = 30%

 

Utilizando a fórmula:

P (A ∪ B) = P(A) + P(B) – P(A ∩ B)

0,8 = 0,4 + P(B) – 0,3

0,8 – 0,4 + 0,3 = P(B)

P(B) = 0,7 = 70%

 

Resposta: A

 

 

Espero que tenham gostado dos nossos exercícios resolvidos sobre a probabilidade da união de dois eventos.

Saber Matemática, o melhor site de matemática para concursos.