Nesta página apresentaremos uma seleção especial de exercícios resolvidos sobre números primos.
O conteúdo é bem interessante e é muito utilizado em problemas que envolvem fatoração e divisibilidade.
Bom estudo e boa sorte!
Questão 1 (PM AC 2012 – Funcab). Determine o produto dos cinco primeiros números primos, quando dispostos em ordem crescente.
A) 2310
B) 720
C) 30030
D) 2520
E) 15015
Resolução:
Para resolver a questão, basta recordarmos quais são os 5 primeiros números primos.
São eles: 2, 3, 5, 7 e 11.
Multiplicando:
2.3.5.7.11 = 2310
Resposta: A
Questão 2 (BB 2015). O número natural abaixo é divisível por:
![]()
(A) 6
(B) 10
(C) 14
(D) 22
(E) 26
Resolução:
Colocando o fator comum em evidência:
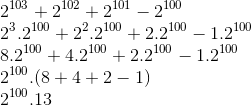
Nota-se que só existem fatores primos 2 e 13, de onde podemos descartar todas as opções, exceto a letra E.
Questão 3 (Bombeiros AC 2012). Determine o valor de n/2, sabendo que é o número de divisores naturais de 3000.
A) 3
B) 4
C) 8
D) 16
E) 24
Resolução:
Vamos calcular a quantidade de divisores naturais de 3000. Para tanto, vamos fatorá-lo:
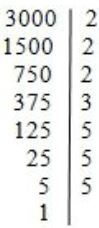
3000 = 2³3¹.5³
Para calcular o número de divisores, basta somar 1 a cada expoente e depois multiplicá-los:
n = 4.2.4 = 32
Como a questão pede n/2:
n/2 = 16
Questão 4 (PM AC 2012 – Músico). Sendo D o número de divisores naturais de 252, e N o número de divisores naturais de 1296, então o valor de 2.D + 3.N será:
A) 18
B) 25
C) 43
D) 75
E) 111
Resolução:
Vamos calcular a quantidade de divisores de cada um dos números. Para isso precisamos fatorá-los:
252 = 2.2.3.3.7
1296 = 2.2.2.2.3.3.3.3
Para saber o número de divisores, basta somar 1 a cada expoente e multiplicá-los:
252 tem 3.3.2 = 18 divisores
1296 tem 5.5 = 25 divisores
Assim, 2.D + 3.N:
2.18 + 3.25 = 36 + 75 = 111

Eu não entendi essa quarta questão?