Apresentamos nesta página vários exercícios resolvidos sobre a multiplicação de matrizes, todos retirados das mais variadas provas de concursos realizados nos últimos anos.

O ideal é que o aluno já tenha acompanhado nosso conteúdo sobre o assunto e também sobre a definição e propriedades das matrizes.

Bom estudo!

 

 

Questão 1 (Prefeitura de Venda Nova do Imigrante – CONSULTPLAN 2016). Calcular o valor de x + y + z, sabendo que:

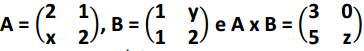
A) 1.

B) 2.

C) 3.

D) 4.

 

Resolução

Vamos utilizar os nossos conhecimentos sobre multiplicação de matrizes, onde C é a matriz resultado do produto AxB:

 

Calculando o elemento c₁₂:

c₁₂ = 2.y + 1.2

0 = 2y + 2

2y = -2

y = -1

 

Calculando o elemento c₂₁:

c₂₁ = x.1 + 2.1

5 = x + 2

x = 5 – 2

x = 3

 

Calculando o elemento c₂₂:

c₂₂ = x.y + 2.2

z = 3.(-1) + 4

z = -3 + 4

z = 1

 

Assim, x+y+z = -1 + 3 + 1 = 3

Resposta: C

 

 

Questão 2 (Prefeitura de Santo André SP – IBAM 2015). Considere as seguintes matrizes:

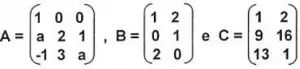
Sendo “a” um número real, para que tenhamos A . B = C, o valor da variável “a” deverá ser:

a) um número inteiro, ímpar e primo.

b) um número inteiro, par, maior que 1 e menor que 5.

c) um número racional, par, maior que 5 e menor que 10.

d) um número natural, impar, maior que 1 e menor que 5.

 

Resolução:

O objetivo da questão é achar o valor do número real “a”, que faz com que a multiplicação A.B = C seja válida.

Vamos verificar o elemento c₂₁:

c₂₁ = a.1 + 2.0 + 1.2

9 = a + 0 + 2

a = 9 – 2

a = 7

 

Podemos fazer o mesmo cálculo para os elementos c₂₁, c₂₂, c₃₁ e c₃₂ que o valor de “a” também será 7, que é m número inteiro, ímpar e primo.

Resposta: A

 

 

Questão 3 (AGU – IDECAN 2014). Dadas as matrizes A = ( a_ij)2×3 em que a_ij = i – j e B = ( b_ij)3×2 em que b_ij = i² – j. Seja a matriz C a matriz resultante do produto das matrizes A e B, nesta ordem. Assim, o elemento c₁₁ será

a) 17

b) 18

c) 19

d) -18

e) -19

 

Resolução:

O primeiro passo para resolver a questão é descobrirmos como são as matrizes A e B.

 

Como em um elemento a_ij, i representa a linha e j a coluna, podemos concluir que cada elemento de A é a diferença entre a linha e a coluna onde o mesmo está localizado. Assim:

a₁₁ = 1 – 1 = 0

a₁₂ = 1 – 2 = -1

a₁₃ = 1 – 3 = -2

a₂₁ = 2 – 1 = 1

a₂₂ = 2 – 2 = 0

a₂₃ = 2 – 3 = -1

Veja como fica a matriz A:

 

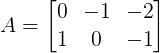
Da mesma forma, vamos calcular cada elemento da matriz B, onde b_ij = i² – j:

_b11 = 1² – 1 = 0

b₁₂ = 1² – 2 = -1

b₂₁ = 2² – 1 = 3

b₂₂ = 2² – 2 = 2

b₃₁ = 3² – 1 = 8

b₃₂ = 3² – 2 = 7

Veja como fica a matriz B:

 

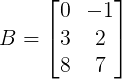
Calculando o elemento c₁₁, onde A.B = C:

c₁₁ = 0.0 + (-1).3 + (-2).8

c₁₁ = 0 – 3 – 16

c₁₁ = -19

 

Resposta: E

 

 

Questão 4 (AGU – IDECAN 2014). Seja A uma matriz 2 x 3 e B uma matriz 3 x 2. A matriz C, resultante do produto da matriz A pela B, nesta ordem, é uma matriz de ordem

a) 2 x 2.

b) 2 x 3.

c) 3 x 2.

d) 3 x 3.

e) Não é possível fazer o produto.

 

Resolução

Para sabermos se é possível multiplicarmos duas matrizes, basta verificarmos se a quantidade de colunas da primeira é igual a quantidade de linhas da segunda. Neste caso são iguais, ambas são iguais a 3.

O número de linhas e colunas da matriz resultante do produto A.B será o número de linhas de A e o número de colunas de B, ou seja, teremos uma matriz 2×2.

Resposta: A

 

 

Questão 5 (PM ES – AOCP). Considere as duas matrizes A e B a seguir:

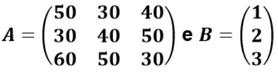
Cada linha da matriz A indica a pontuação obtida, em cada tentativa, em uma prova de tiro ao alvo por um competidor. Assim, a primeira linha indica as pontuações do competidor X, a segunda linha indica as pontuações do competidor Y e a terceira linha indica as pontuações do competidor Z. Obtendo-se uma matriz C = A.B, na matriz C aparece a nota de desempenho final de cada um dos três competidores X, Y e Z, respectivamente, na primeira, na segunda e na terceira linha. Dessa forma, é correto afirmar que

(A) o competidor X obteve a menor nota de desempenho final, igual a 250.

(B) o competidor Y obteve a maior nota de desempenho final, igual a 260.

(C) o competidor Z obteve a menor nota de desempenho final, igual a 230.

(D) os competidores X e Y obtiveram a mesma nota de desempenho final.

(E) os competidores X e Z obtiveram a mesma nota de desempenho final.

 

Resolução

Calculando a nota de cada um dos competidores:

X = 50.1 + 30.2 + 40.3 = 50 + 60 + 120 = 230

Y = 30.1 + 40.2 + 50.3 = 30 + 80 + 150 = 260

Z = 60.1 + 50.2 + 30.3 = 60 + 100 + 90 = 250

Resposta: B

 

 

Gostou dos nossos exercícios resolvidos sobre multiplicação de matrizes?

Deixe o seu comentário.