Confira aqui vários exercícios resolvidos sobre matriz transposta, todos retirados de provas de concursos e ENEM.

Bom estudo!

Exercício 1 (ESAF). As matrizes, A, B, C e D são quadradas de quarta ordem. A matriz B é igual a 1/2 da matriz A, ou seja: B = (1/2).A. A matriz C é igual a matriz transposta de B, ou seja: C = B^t . A matriz D é definida a partir da matriz C; a única diferença entre essas duas matrizes é que a matriz D tem como primeira linha a primeira linha de C multiplicada por 2.

Sabendo-se que o determinante da matriz A é igual a 32, então a soma dos determinantes das matrizes B, C e D é igual a

A) 6.

B) 4.

C) 12.

D) 10.

E) 8.

Resolução

Sabemos que detA = 32.

Como B = (1/2).A, podemos utilizar uma das propriedades dos determinantes: det(k.A) = kⁿ . detA.

Neste caso, temos k = 1/2 e n = 4 (todas as matrizes são de quarta ordem).

detB = det(k.A) = kⁿ . detA = (1/2)⁴.32 = 2

Como a matriz C é a transposta de B, ou seja, C = B^t , podemos utilizar outra propriedade: detA = det(A^t).

detC = det(B^t) = detB = 2

Como a matriz D é definida a partir da matriz C; a única diferença entre essas duas matrizes é que a matriz D tem como primeira linha a primeira linha de C multiplicada por 2, podemos utilizar outra propriedade:

detD = 2.detC = 2.2 = 4

Temos:

• detB = 2
• detC = 2
• detD = 4

Total: 2 + 2 + 4 = 8

Resposta: E

Exercício 2 (FCC). Um estudante está procurando uma matriz quadrada M, de ordem 2 × 2, tal que M.M^t seja igual à matriz identidade de ordem 2 × 2, sendo M^t a matriz transposta de M. Uma matriz que atende às condições do estudante é M igual a

Resolução

Considere as matrizes M e M^t, sendo que M^t é a matriz transposta de M:

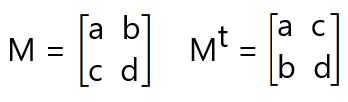
Multiplicando as duas matrizes:

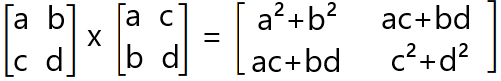
E sabendo que o produto deve ser igual a matriz identidade:

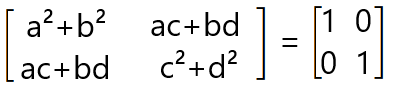
Nota-se que:

• a² + b² = 1
• ac + bd = 0
• c² + d² = 1

Como a² + b² = 1, podemos descartar as opções A, D e E.

Como ac + bd = 0, podemos descartar a letra C.

Basta conferir a matriz da letra B:

a² + b² = cos²θ + (-senθ)² = cos²θ + sen²θ = 1

ac + bd = cosθ.senθ + (-senθ).cosθ = cosθ.senθ – cosθ.senθ = 0

c² + d² = sen²θ + cos²θ = 1

Resposta: B

Gostou dos nossos exercícios resolvidos sobre matriz transposta?

Deixe o seu comentário.