Olá amante da matemática! Confira aqui vários exercícios resolvidos sobre as inequações do 1° (primeiro) grau. O ideal é que você tenha estudado o material didático sobre esse conteúdo.

Lembrando que todas as questões foram retiradas de concursos públicos realizados pelo país.

Boa sorte a todos!

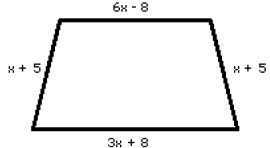
Questão 1 (PM Pará). Baseado na figura abaixo, o menor valor inteiro par que o número x pode assumir para que o perímetro dessa figura seja maior que 80 unidades de comprimento é:

a) 6

b) 8

c) 10

d) 12

e) 14

Resolução:

Calculando o perímetro (lembrando que o perímetro é a soma de todos os lados):

P = x + 5 + 3x + 8 + x + 5 + 6x -8

P = 11x + 10

Queremos que 11x + 10 seja maior que 80.

11x + 10 > 80

Resolvendo a inequação do 1° grau:

11x + 10 > 80

11x > 80 – 10

x > 70/11

x > 6,36

O menor inteiro par será 8.

Resposta: B

Questão 2 (CBM-RJ). A solução de 4 – 3x > -2 é:

a) x < 2

b) x < 1

c) x < 6

d) x > 2

e) x > 6

Resolvendo a inequação do 1° (primeiro) grau:

4 – 3x > -2

– 3x > -2 – 4

– 3x > -6

3x < 6

x < 6/3

x < 2

Resposta: A

Questão 3 (CMB – Cesgranrio). Qual é o menor valor inteiro que satisfaz a desigualdade apresentada a seguir?

9x + 2(3x – 4) > 11x – 14

a) -2

b) -1

c) 0

d) 1

e) 2

Resolvendo a inequação do 1° (primeiro) grau:

9x + 2(3x – 4) > 11x – 14

9x + 6x – 8 > 11x – 14

15x – 8 > 11x – 14

15x – 11x > – 14 + 8

4x > – 6

x > -6/4

x > -3/2

Como -3/2 = -1,5, o menor valor inteiro que satisfaz a inequação é -1.

Resposta: B

Questão 4 (CAERN – FGV). O conjunto de todas as soluções reais da inequação 2x + 1 < 3x + 2 é

a) ]-∞, -1[

b) ]-∞, 1[

c) ]-1, +∞[

d) ]1, +∞[

e) ]-1, 1[

Resolvendo a inequação do 1° (primeiro) grau:

2x + 1 < 3x + 2

2x – 3x < 2 – 1

-x < 1

x > -1

A solução da inequação é o conjunto de números reais maiores que -1.

S = ]-1, +∞[

Resposta: C

Questão 5 (UP). Em R, qual é a solução da inequação

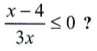
a) ]-∞; 4]

b) ]-∞; 0[ ∪ [4; +∞[

c) ]0; 4]

d) [4; +∞[

Resolução

Observe que a inequação apresenta uma divisão de duas funções:

f(x) = x – 4

g(x) = 3x

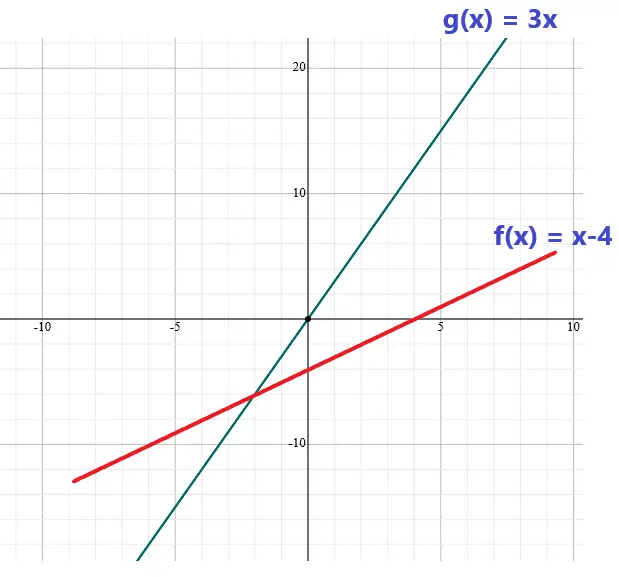
f(x) > 0 quando x > 0

g(x) > 0 quando x > 4

Teremos f(x)/g(x) ≤ 0 quando as funções possuírem sinais contrários, ou seja, x deve estar entre 0 e 4.

Para finalizar, devemos analisar os extremos:

0 não pode ser solução da inequação pois teríamos uma divisão por zero, que não está definida.

4 é solução da inequação, pois teríamos f(x)/g(x) = 0 ≤ 0.

Solução: ]0; 4]

Resposta: C

Gostou dos exercícios resolvidos sobre inequações do 1° grau?

Deixe seu comentário e compartilhe nas redes sociais.