Confira aqui vários exercícios resolvidos sobre a função modular, todos retirados das últimas provas de concursos públicos.
Bom estudo!
Exercício 1 (Marinha). Dada a função f(x ) = √|x|, no intervalo [- 2,1], determine o valor de x, onde a função atinge seu valor máximo, e assinale a opção correta.
A) x = -2
B) x = – 1/4
C) x = 0
D) x = 1/2
E) x = 1
Resolução
A função atingirá o seu valor máximo quando o módulo |x| atingir o seu valor máximo.
Sabendo que o domínio da função é o intervalo [- 2,1], o valor máximo será atingido quando x = -2.
Isso pode ser constatado através do gráfico da função:
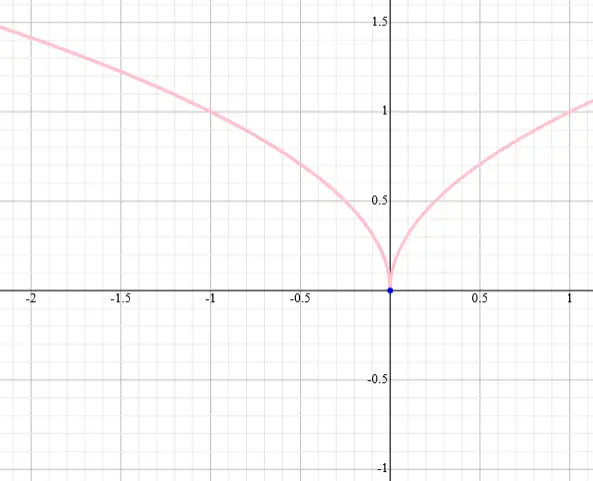
Resposta: A
Exercício 2 (Espcex). Sabendo que o gráfico a seguir representa a função real f(x)=|x-2|+|x+3|, então o valor de a + b + c é igual a
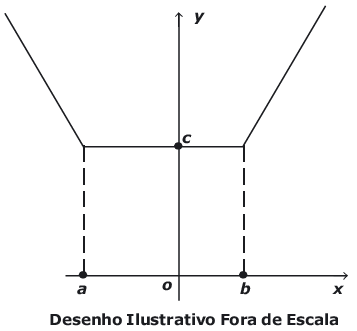
a) -7
b) -6
c) 4
d) 6
e) 10
Resolução
A função modular f(x)=|x-2|+|x+3| pode ser resolvida através da análise dos termos |x-2| e |x+3|.
Veja que:
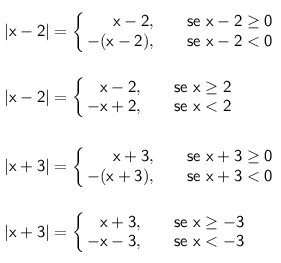
Temos três intervalos a considerar:
- x < -3
f(x) =|x-2|+|x+3|
f(x) = (- x + 2) + (- x – 3)
f(x) = – x + 2 – x – 3
f(x) = – 2x – 1
- −3 ≤ x < 2
f(x) =|x-2|+|x+3|
f(x) = (- x + 2) + (x + 3)
f(x) = – x + 2 + x + 3
f(x) = 5
- x ≥ 2
f(x) =|x-2|+|x+3|
f(x) = (x – 2) + (x + 3)
f(x) = x – 2 + x + 3
f(x) = 2x + 1
Observe que:
- o valor de c representa a função constante onde −3 ≤ x < 2, ou seja, c = 5;
- a e b são os valores de x onde a função sofre alterações, ou seja, a = -3 e b = 2.
Total: a + b + c = -3 + 2 + 5 = 4
Resposta: C
Exercício 3 (ESPP). A função ƒ(x) = |x² – 4x| é decrescente no intervalo:
a) ]-∞,2 [ ∪] 4, +∞[
b) ]-∞,0 [ ∪] 2,4[
c) ]-∞,0 [ ∪] 4, +∞[
d) ]-∞,2 [
Resolução
Antes de analisarmos a função modular, veremos o formato da função quadrática g(x) = x² – 4x.
Como trata-se de uma função incompleta, onde c = o, temos:
x² – 4x = 0
x(x – 4) = 0
x = 0 ou x = 4
Sabendo que o gráfico é representado por uma parábola, e que as raízes são 0 e 4, o gráfico da função g(x) terá o seguinte formado:
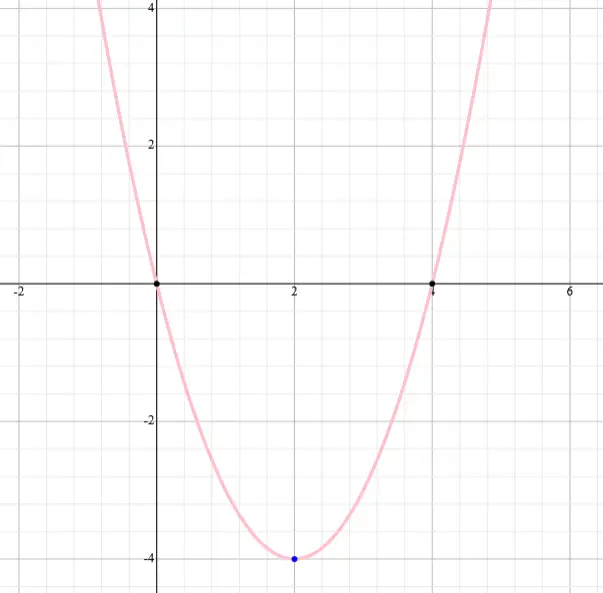
Vejamos agora o que acontece quando aplicamos o módulo à função g(x) = x² – 4x.
Observe que o módulo altera o sinal da parte negativa, ou seja, o intervalo do gráfico em que g(x)<0 torna-se positivo, de forma simétrica ao eixo x.
Gráfico da função f(x):
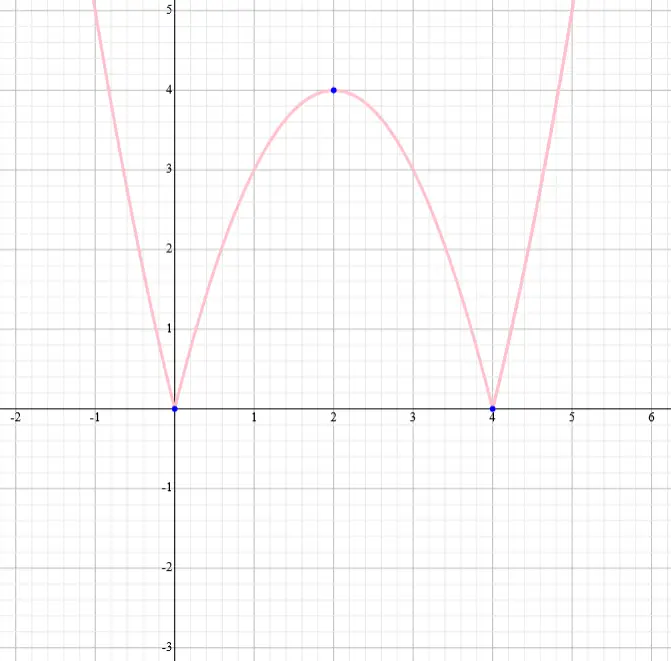
Podemos observar no gráfico que a função f(x) é decrescente nos intervalos ]-∞,0 [ e ] 2,4[.
Resposta: B
Questão 4 (EEAR). Seja f(x) = |3x – 4| uma função. Sendo a ≠ b e f(a) = f(b) = 6, então o valor de a + b é igual a
A) 5/3
B) 8/3
C) 5
D) 3
Resolução
Observe que:
3x – 4 = 0
3x = 4
x = 4/3
Considerando que temos uma função modular, temos dois casos a considerar:
- f(x) = -3x + 4, se x < 4/3
- f(x) = 3x – 4, se x ≥ 4/3
Sendo a ≠ b e f(a) = f(b) = 6, podemos concluir que são dois valores de x distintos, cuja imagem é igual a 6.
Igualando os dois casos anteriores a 6, temos:
-3x + 4 = 6
-3x = 6 – 4
– 3x = 2
x = -2/3 (valor de a)
3x – 4 = 6
3x = 6 + 4
3x = 10
x = 10/3 (valor de b)
Total:
a + b = -2/3 + 10/3 = 8/3
Resposta: B
Gostou dos nossos exercícios resolvidos sobre função modular?
Deixe o seu comentário.
