Procurando exercícios resolvidos sobre as equações trigonométricas? Chegou ao site certo. Aqui você encontra exercícios retirados dos últimos concursos públicos.
O ideal é que o aluno já possua um bom conhecimento acerca das equações e das funções trigonométricas.
Bom estudo!
Exercício 1. (Bombeiros MG 2008 – Igetec). As soluções da equação trigonométrica sen(2x) – 1/2 = 0, que estão na primeira determinação são:
a) x = π/12 ou x = 3π/24
b) x = π/12 ou x = 5π/12
c) x = π/6 ou x = 3π/12
d) x = π/6 ou x = 5π/24
Resolução:
sen(2x) – 1/2 = 0
sen(2x) = 1/2
Os arcos cujo seno é 1/2 são π/6 e 5π/6.
Assim, temos dois casos a considerar:
Caso 1:
2x = π/6
x = π/12
Caso 2:
2x = 5π/6
x = 5π/12
Resposta: B
Exercício 2 (Câmara FJC – FIP 2009). Se sen(x) = 3/5, com 0≤x≤π/2, então o valor de cotg(x) é:
a) 1/2
b) 4/3
c) 4/5
d) 1
e) 3/4
Resolução:
Como sen(0°)=0 e sen(π/2)=1, vamos considerar x um ângulo maior que 0º e menor que 90°.
Sabendo que sen(x) = 3/5, e que seno é a razão entre o cateto oposto e a hipotenusa do triângulo onde x está localizado, e mais ainda, que todos os triângulos com essas características são semelhantes, vamos resolver a questão analisando o triângulo retângulo abaixo:
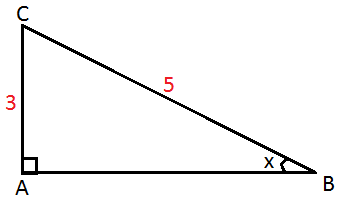
Vamos calcular o valor de AB através do teorema de pitágoras:
5² = 3² + AB²
25 = 9 + AB²
AB² = 25 – 9
AB = √16
AB = 4
Basta agora calcularmos a cotg(x). Lembrando que ela representa o inverso da tangente de x:
![]()
Resposta: B
Exercício 3. Qual o conjunto solução da equação trigonométrica abaixo?
2.sen(3x) + 1 = 0
Resolução:
2.sen(3x) + 1 = 0
2.sen(3x) = – 1
sen(3x) = – 1/2
No ciclo trigonométrico existem dois arcos entre 0 e 2π cujo seno é igual a -1/2. São eles:
sen(-π/6) = -1/2
sen(7π/6) = -1/2
Assim,
3x = 7π/6 + 2kπ ou 3x = – π/6 + 2kπ, k∈Z.
Logo,
x = 7π/18 + 2kπ/3 ou x = – π/18 + 2kπ/3
De onde concluímos que o nosso conjunto solução será:
S = {x∈R / x = 7π/18 + 2kπ/3 ou x = – π/18 + 2kπ/3, k∈Z}
Exercício 4. Resolver a equação senx + cosx = 1.
Elevando ambos os membros ao quadrado:
(senx + cosx)² = 1²
(senx)² + 2.senx.cosx + (cosx)² = 1
(senx)² + (cosx)² + 2.senx.cosx = 1
Utilizando a relação fundamental da trigonometria:
1 + 2.senx.cosx = 1
2.senx.cosx = 0
sen(2x) = 0
Daí,
2x = kπ, k∈Z
x = (π/2).k, k∈Z
Exercício 5. Resolver a equação trigonométrica tg x = √3.
Resolução
Podemos afirmar que x = π/3 é uma solução, considerando que tg(π/3) = √3
Logo, o conjunto solução será:
S = {x∈R | x = π/3 + kπ, k∈Z}
Por Favor, como resolver essa equação, sei que o resultado possível é x=90 graus. Porém como provar matematicamente.
-2x + sen 2x = -180
-2x+sen2x=-180 / -2x+2senxcosx=-180/ 2(-x+senxcosx)=-180/-x+senxcosx=-90/x-senxcosx=90/sen90=1/cos90=0/x=90.
Bom dia! Por favor, como posso resolver as seguintes equações:
a) Seno(x−pi/3 )=√3/2
b) Cos2x−√2/2 =0
c) tan2x= √3 .
d) Determine x tal que 0 < x < 2pi e cos2x=1/2
Como chegar nesse valor x=90?
Olá Geraldo!
Está se referindo a qual questão?
Como resolver
Cotgx+tgx=2
Olá Estevão!
Cotgx+tgx=2
cosx/senx + senx/cosx = 2
tirar o mmc
utilizar a relação:
sen2x = 2senx.cosx
2senx= √3
Sen(x)= √3/2
X= 60(Graus). Ou x=π\3
2sinX-√2=0 ; x € [0°;180°]
oi como posso reslver estas equações
tag x =1
sen 2x= 1/2
2cos 3x= raiz quadrada 2
3cotg 5x=1
cossec x= raiz 2
sec 2x=2
2sen x -6sen x-8=0
sen x – sen x=0
Como resolver
Cos (2x)+senx=0