Procurando exercícios resolvidos sobre a equação reduzida da circunferência? Confira aqui várias questões comentadas, todas retiradas das últimas provas de concursos públicos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria analítica.
Questão 1 (EsSA 2013). Dada a equação da circunferência é: (x-a)² + (y-b)² = r², sendo (a, b) as coordenadas do centro e r a medida do raio, identifique a equação geral da circunferência de centro (2 , 3) e raio igual a 5.
a) x² + y² = 25
b) x² + y² – 4xy – 12 = 0
c) x² – 4x = -16
d) x² + y² – 4x – 6y – 12 = 0
e) y² – 6y = -9
Resolução
A questão informa que o centro é (2, 3) e o raio é igual a 5. Temos:
(x – a)² + (y – b)² = r²
(x – 2)² + (y – 3)² = 5²
x² – 4x + 4 + y² – 6y + 9 = 25
x² – 4x + 4 + y² – 6y + 9 – 25 = 0
x² + y² – 4x – 6y – 12 = 0
Resposta: D
Questão 2 (SEDUC RJ – CEPERJ 2013). Seja (x – 2)² + (y – 4)² = 8 a equação reduzida de uma circunferência. A razão entre a área da circunferência e a área do quadrado inscrito na circunferência, nesta ordem, é:
a) π/4
b) π/2
c) π
d) 3π/2
e) 3π
Resolução
Nosso objetivo será descobrir a área da circunferência e do quadrado inscrito, para então efetuarmos a divisão.
A informação mais importante que a equação reduzida da circunferência nos dá é que o raio é igual a √8.
Calculando a área da circunferência:
A = π.r² = π.(√8)² = 8π
Vamos descobrir a medida dos lados (x) do quadrado utilizando o Teorema de Pitágoras.
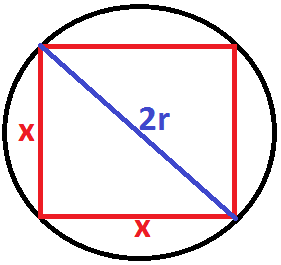
(2r)² = x² + x²
(2√8)² = 2x²
4.8 = 2x²
32 = 2x²
x² = 16
x = 4
Calculando a área do quadrado:
A = x² = 4² = 16
Calculando a razão entre a área da circunferência e a área do quadrado:
8π/16 = π/2
Resposta: B
Gostou dos nossos exercícios resolvidos sobre a equação reduzida da circunferência?
Deixe o seu comentário.
