Estudando matemática e estatística para concursos? Confira aqui vários exercícios resolvidos sobre a distribuição de Poisson, todos retirados dos últimos concursos públicos.
Não deixe de ver em nosso menu outras publicações com exercícios resolvidos de vários tópicos da matemática e estatística.
Bom estudo!
Questão 1 (RFB – Esaf 2009). O número de petroleiros que chegam a uma refinaria ocorre segundo uma distribuição de Poisson, com média de dois petroleiros por dia. Desse modo, a probabilidade de a refinaria receber no máximo três petroleiros em dois dias é igual a:
Resolução
Veja abaixo a fórmula para se determinar a probabilidade de um dado número X de sucessos em uma distribuição de Poisson. Onde e = 2,71828… é a constante de Euler.
![]()
A média é de dois petroleiros por dia. Obviamente, a cada dois dias, teremos uma média de 4 petroleiros, logo λ=4.
Calculando a probabilidade da plataforma receber no máximo 3 petroleiros em 2 dias:
P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3)
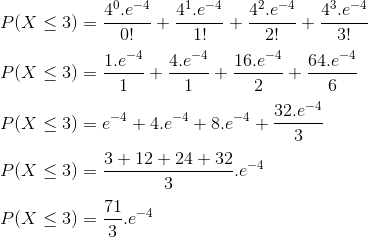
Resposta: C
Questão 2 (ANAC – Esaf 2016). Uma distribuição Binomial pode ser aproximada por uma distribuição de Poisson, quando a probabilidade do evento é pequena de ocorrer e a população considerada é relativamente grande. Assuma esta aproximação para o problema descrito a seguir. Considere que passageiros chegam a um aeroporto a uma taxa média de três passageiros por segundo. Pede-se para determinar, com uma boa aproximação, qual a probabilidade (P) de que não mais de dois passageiros chegarão ao aeroporto em um intervalo de um segundo (caso seja necessário, use o valor de e=exp(1) = 2,72).
a) P = 0,28.
b) P = 0,22.
c) P = 0,36.
d) P = 0,25.
e) P = 0,42.
Resolução
A questão pede a probabilidade de chegarem não mais de 2 passageiros em um intervalo de um segundo, assim, utilizaremos a fórmula da distribuição de Poisson para calcular a probabilidade de chegarem até 2 passageiros em um intervalo de um segundo.
P(X≤2) = P(X=0) + P(X=1) + P(X=2)
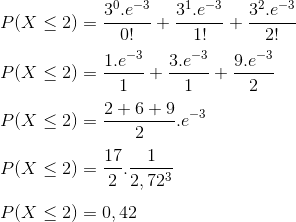
Resposta: E
Questão 3 (SEFAZ PI – FCC 2015). O número de falhas mensais de um computador é uma variável que tem distribuição de Poisson com média λ. Sabe-se que λ é igual à média de uma distribuição uniforme no intervalo [2, 4]. Nessas condições, a probabilidade de o computador apresentar exatamente duas falhas no período de 15 dias é igual a:
Dados: e-3 = 0,05; e-1,5 = 0,22.
a) 22,50%
b) 12,50%
c) 24,15%
d) 15,25%
e) 24,75%
Resolução
A média de uma distribuição uniforme no intervalo [a, b] é a média aritmética dos valores a e b. Assim, a média da distribuição uniforme no intervalo [2, 4] é dada por:
(2 + 4)/2 = 3
Veja que o valor encontrado corresponde ao período de um mês, ou seja, a média de falhas a cada 15 dias é igual a 1,5.
Como a questão pede a probabilidade do computador apresentar exatamente duas falhas no período de 15 dias, utilizaremos a fórmula da distribuição de Poisson, onde λ=1,5 e X=2:
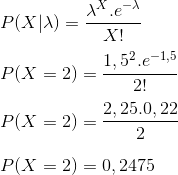
Resposta: E
Questão 4 (SEFAZ PE – FCC 2014). Para resolver a questão abaixo, considere as informações a seguir:
Se Z tem distribuição normal padrão, então: P(Z < 1,64) = 0,950; P(Z < 2,05) = 0,98; P(Z < 2,24) = 0,987; P(Z < 2,40) = 0,992.
Suponha que o número de pedidos de empréstimos que um banco recebe por dia seja uma variável com distribuição de Poisson com média de λ pedidos por dia. Sabe-se que o parâmetro λ satisfaz à equação P(X < λ) = 0,008, onde X é uma variável aleatória que tem distribuição normal com média 15 e variância 25. Nessas condições, a probabilidade de o banco receber, em um dia qualquer, exatamente 4 pedidos de empréstimo
Dados: e-3 = 0.05; e-4 = 0,018
a) está compreendida entre 20% (inclusive) e 22% (exclusive).
b) é maior do que 25%.
c) é menor do que 16%.
d) está compreendida entre 16% (inclusive) e 18% (exclusive).
e) está compreendida entre 18% (inclusive) e 20% (exclusive).
Resolução
Sabendo que temos uma distribuição normal padrão, com P(Z < 2,40) = 0,992, podemos concluir que P(Z < -2,40) = 0,008).
Como a variância é igual a 25, podemos concluir que o desvio padrão é igual a 5.
Z = (λ – μ)/σ
-2,40 = (λ – 15)/5
-12 = λ – 15
λ = 3
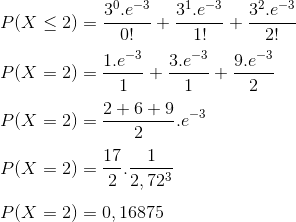
Resposta: D
Gostou dos nossos exercícios resolvidos sobre a distribuição de Poisson?
Deixe o seu comentário.

O número de pessoas que semanalmente apresenta um pe- dido de emprego no Centro de Emprego de Setúbal é uma variável aleatória que segue uma distribuição Poisson com E[X] = 9. Cerca de 80% das pessoas pretendem trabalhar no sector dos serviços.
1. Qual a probabilidade de em determinada semana não aparecerem mais de 4 pedidos no centro de emprego?
2. Tendo seleccionado 12 dos pedidos recepcionados, qual a probabilidade de se encontrarem mais de 7 dirigidos a sectores que não o de serviços?
Muito bom esses exercícios, parabéns galera do SaberMatematica e muito obrigado!!
Calcular a espessura “a” tal que P(X < a) = 3P(X =< a)