Estudando matemática para concursos? Confira vários exercícios resolvidos sobre ângulos, todos retirados dos últimos concursos.

Não deixe de ver também em nosso menu as publicações sobre outros tópicos da geometria.

Bom estudo!

 

 

Questão 1 (SAP SP). Um arquiteto, em um de seus projetos, fez algumas medições e dentre elas mediu dois ângulos complementares. Um desses ângulos mediu 65º e o outro,

(A) 115º.

(B) 90º.

(C) 180º.

(D) 25º.

(E) 60º.

 

Resolução

Dois ângulos são ditos complementares quando a soma da medida de ambos é igual a 90º.

Seja x a medida do ângulo desconhecido:

x + 65 = 90

x = 90 – 65

x = 25º

Resposta: D

 

 

Questão 2 (VUNESP – Prefeitura de Marília – SP). Dois quadrados foram construídos sobre os lados de um losango e um triângulo foi construído a partir dos lados desses quadrados, conforme mostra a figura.

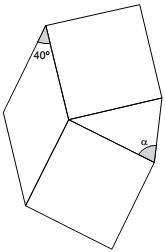
A medida do ângulo α é

a) 50º.

b) 55º.

c) 60º.

d) 65º.

e) 70º.

 

Resolução

Observe na figura abaixo que:

• Em um losango, os ângulos opostos são iguais, e a soma dos ângulos internos é igual a 360º, ou seja, dois ângulos medem 40º e os outros dois medem 140º.
• Um quadrado possui todos os ângulos iguais a 90º.
• Uma “volta completa” equivale a um ângulo de 360º, de onde concluímos que um dos ângulos do triângulo mede 40º.
• Como o triângulo é isósceles (dois lados iguais) e a soma dos ângulos internos é igual a 180º, podemos concluir que os demais ângulos medem 70º, ou seja, α = 70º.

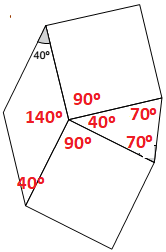
Resposta: E

 

 

Questão 3 (CETESB – VUNESP). A figura mostra um canteiro retangular dividido em quatro partes onde a, b e c são as medidas dos ângulos assinalados.

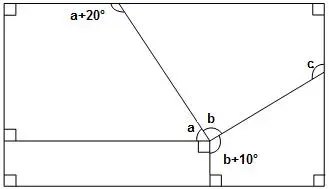
Os valores de a, b e c, são, respectivamente,

a) 80°, 90° e 100°.

b) 80°, 90° e 110°.

c) 90°, 80° e 100°.

d) 90°, 100° e 80°.

e) 110°, 90° e 80°.

 

Resolução

Sabendo que a soma dos ângulos internos de um quadrilátero é igual a 360º, temos:

90º + (a + 20º) + 90º + a = 360º

2a + 200º = 360º

2a = 360º – 200º

2a = 160º

a = 160º/2

a = 80º

 

Sabendo que um ângulo completo mede 360º, temos:

a + b + (b + 10º) + 90º = 360º

80º + 2b + 100º = 360º

2b + 180º = 360º

2b = 360º – 180º

2b = 180º

b = 180º/2

b = 90º

 

Sabendo que a soma dos ângulos internos de um quadrilátero é igual a 360º e que o complementar do ângulo a+20º é igual a 80º, temos:

80º + 90º + b + c = 360º

80º + 90º + 90º + c = 360º

260º + c = 360º

c = 360º – 260º

c = 100º

 

Resposta: A

 

 

Questão 4 (Câmara de Lagoa da Prata – MG – FUMARC). Se os ângulos internos de um triângulo estão em Progressão Aritmética de razão 40º, então é CORRETO afirmar que a medida do menor ângulo agudo desse triângulo é igual a:

a) 20º

b) 40º

c) 60º

d) 80º

 

Resolução

Sabendo que os três ângulos internos de um triângulo estão em P.A. de razão 40º, temos que cada um deles mede:

x – 40º, x, x + 40º

 

Como a soma é sempre igual a 180º, temos:

(x – 40º) + x + (x + 40º) = 180º

x – 40º + x + x + 40º = 180º

3x = 180º

x = 180º/3

x = 60º

 

Daí, os ângulos medem 20º, 60º e 100º.

Resposta: A

 

 

Questão 5 (Prefeitura de Taquarituba – SP – Instituto Excelência). Analise a figura abaixo, classifique o ângulo indicado e assinale a alternativa CORRETA:

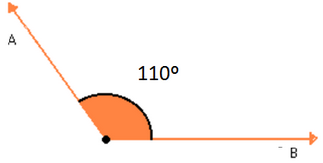
a) Ângulo obtuso.

b) Ângulo agudo

c) Ângulo reto.

d) Nenhuma das alternativas.

 

Resolução

Um ângulo é chamado de obtuso sempre que a sua medida for maior que 90º e menor que 180º.

Resposta: A

 

 

Questão 6 (Prefeitura de Goiânia – UFG). Considere que a figura abaixo representa um relógio analógico cujos ponteiros das horas (menor) e dos minutos (maior) indicam 3 h e 40 min.

Nestas condições, a medida do menor ângulo, em graus, formado pelos ponteiros deste relógio, é:

a) 120

b) 126

c) 130

d) 132

 

Sabendo que um ângulo completo mede 360º, e que o relógio está dividido em 12 horas, temos que cada hora é equivalente a:

360º/12 = 30º

Veja que entre 4 e 8 horas, temos:

4.30º = 120º

 

O horário marcado pelo relógio é de 3 h e 40 min, ou seja, o ponteiro menor já percorreu 2/3 da distância entre 3 e 4 horas, restando ainda 1/3.

30°.1/3 = 10º

 

Total: 120º + 10º = 130º

Resposta: C

 

 

Questão 7 (MGS). Observe os ponteiros nesse relógio.

Decorridas 3 horas, qual é o ângulo formado pelos ponteiros?

a) 15º

b) 45º

c) 90º

d) 180º

 

Resolução

Veja que o relógio marca 12 horas, ou seja, após 3 horas, o ponteiro menor estará sobre o 3 e o maior sobre o 12.

Como cada hora do relógio equivale a 30º, temos:

3.30º = 90º.

Resposta: C

 

 

Questão 8 (Prefeitura de Tarrafas – CE – CONSULPAM). Dois ângulos suplementares medem respectivamente 3x − 40º e 2x + 60º. O menor desses ângulos mede:

a) 108º

b) 132º

c) 124º

d) N.D.A

 

Dois ângulos são suplementares quando a soma é igual a 180º.

(3x − 40º) + (2x + 60º) = 180º

3x − 40º + 2x + 60º = 180º

5x + 20º = 180º

5x = 180º – 20º

5x = 160º

x = 160º/5

x = 32º

 

Calculando a medida de cada um dos ângulos:

3x − 40º = 3.32º – 40º = 96º – 40º = 56º

2x + 60º = 2.32º + 60º = 64º + 60º = 124º

 

Veja que o menor ângulo mede 56º.

Resposta: D

 

 

Gostou dos nossos exercícios resolvidos sobre ângulos?

Deixe o seu comentário.