Confira aqui tudo o que você precisa saber sobre os espaços vetoriais, onde apresentaremos a definição e vários exemplos.
Veja também em nosso menu várias publicações sobre outros tópicos da Álgebra Linear.
Bom estudo!
DEFINIÇÃO DE ESPAÇO VETORIAL
Seja V um conjunto no qual estão definidas as operações:
- Adição: Para quaisquer elementos u e v de V, associamos um elemento u+v de V;
- Multiplicação por escalar: Para todo número real α e qualquer elemento v de V, associamos um elemento αv de V.
O conjunto V, onde valem as duas operações elencadas acima, é chamado de Espaço Vetorial se, para todos os elementos u, v, w ∈ V, e α, β ∈ R, todas as 8 condições abaixo são satisfeitas:
- Comutatividade
u + v = v + u
- Associatividade
u + (v + w) = (u + v) + w
- Existência de elemento neutro para a adição
Existe um elemento 0∈V, tal que v+0 = v, para todo v∈V
- Existência de elemento oposto na adição
Para todo v∈V, existe -v, tal que v + (−v) = 0
- Associatividade
α(βv) = (αβ)v
- Distributividade de escalares
(α + β)v = αv + βv
- Distributividade de vetores
α(u + v) = αu + αv
- Existência de elemento neutro para a multiplicação
1·v = v
EXEMPLOS DE ESPAÇOS VETORIAIS
- R²
O primeiro passo para verificarmos que R² é um espaço vetorial é verificar se estão definidas as operações de adição e multiplicação por escalar.
Sejam:
(x1,x2) e (y2,y2) ∈ R2, e α∈R.
(x1,x2) + (y1,y2) = (x1 + y1,x2 + y2)
α(x1,x2) = (αx1,αx2)
O segundo passo é verificar se as 8 condições são satisfeitas.
Sejam:
u = (x1,x2), v = (y1,y2) e w = (z1,z2), elementos de R2
α e β elementos de R
- u + v = (x1 + y1, x2 + y2) = (y1 + x1, y2 + x2) = v + u
- u+(v+w) = (x1 + (y1 + z1), x2 +(y2 + z2)) = ((x1 + y1)+z1,(x2 + y2) + z2) = (u + v) + w
- u + (0,0) = (x1 + 0, x2 + 0) = (x1, x2) = u
- −u = (−x1,−x2), temos u+(−u) = (x1−x1, x2−x2) = (0,0)
- α(βu) = α(βx1, βx2) = (αβx1, αβx2) = (αβ)u
- (α + β)u = ((α + β)x1, (α + β)x2) = (αx1 + βx1, αx2 + βx2) = αu + βu
- α(u+v) = α(x1 +y1, x2 +y2) = (α(x1 +y1),α(x2 +y2)) = (αx1 + αy1, αx2 + αy2) = αu + αv
- 1u = (1x1, 1x2) = (x1, x2) = u
- R³, R4…, Rn
As prova são análogas a R², e deixaremos a cargo do aluno.
- C (Conjunto dos números complexos)
- Polinômios de grau n, onde n é um número natural não nulo
EXEMPLOS DE CONJUNTOS QUE NÃO SÃO ESPAÇOS VETORIAIS
- N (conjunto dos números reais)
Basta verificar que não existe um elemento neutro para a adição.
Não existe n∈N, tal que 5 + n = 0
- Z (conjunto dos números inteiros)
Basta verificar que quanto multiplicamos um número Z por um número irracional, por exemplo √3, o resultado não é um número Z.
5.√3 ∉ Z
Gostou da nossa publicação sobre Espaço Vetorial?
Deixe o seu comentário.
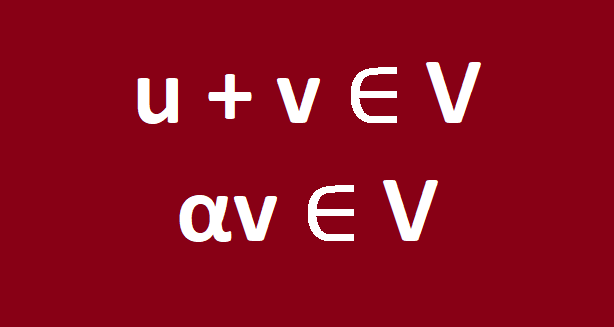
Analise as asserções a seguir:
I. Em um espaço vetorial euclidiano com dimensão finita, a matriz de um operador representando uma isometria tem determinante ±1
porque
II. Se o determinante do operador for diferente de ±1, ele modifica a norma de vetores e, portanto, muda a distância da origem até o vetor.
Assinale a alternativa correta.
a )
As asserções I e II são proposições falsas.
b )
A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
c )
As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa da I.
d )
A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
e )
As asserções I e II são proposições verdadeiras, e a II é uma justificativa da I.