Confira aqui a resolução comentada da questão 142 (análise combinatória) do caderno amarelo, matéria de MATEMÁTICA E SUAS TECNOLOGIAS.
Bom estudo!
Questão 142. Três amigos, André, Bernardo e Carlos, moram em um condomínio fechado de uma cidade. O quadriculado representa a localização das ruas paralelas e perpendiculares, delimitando quadras de mesmo tamanho nesse condomínio, em que nos pontos A, B e C estão localizadas as casas de André, Bernardo e Carlos, respectivamente.
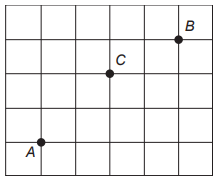
André deseja deslocar-se da sua casa até a casa de Bernardo, sem passar pela casa de Carlos, seguindo ao longo das ruas do condomínio, fazendo sempre deslocamentos para a direita ( → ) ou para cima ( ↑ ), segundo o esquema da figura. O número de diferentes caminhos que André poderá utilizar para realizar o deslocamento nas condições propostas é
A) 4.
B) 14.
C) 17.
D) 35.
E) 48
Resolução
Observe que a localização de B em relação a A é a seguinte:
- 4 ruas à direita
- 3 ruas acima
Isto significa que, qualquer que seja o caminho escolhido por André, o deslocamento utilizará 4 setas para a direita ( → ) e 3 setas para cima ( ↑ ).
Neste caso, a quantidade total de caminhos poderá ser calculada através de uma combinação de 7 elementos, tomados 4 a 4.
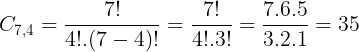
Agora que calculamos a quantidade total de caminhos, devemos analisar a condição de não passar pelo ponto C. Neste caso, calcularemos a quantidade total de caminhos passando por C. Este cálculo deve ser feito em duas etapas:
- Quantidade de caminhos de A até C. Neste caso, devemos ter duas setas para a direita e duas
setas para cima.
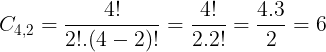
- Quantidade de caminhos de C até B. Neste caso, devemos ter duas setas para a direita e uma
para cima.
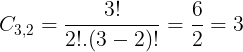
Quantidade de caminhos passando por C:
6 . 3 = 18
Para finalizar, temos 35 caminhos possíveis, sendo que 18 deles passam pelo ponto C:
35 – 18 = 17
Resposta: C
