Procurando exercícios resolvidos sobre determinantes?
Chegou ao site certo.
Aqui a matemática é apresentada de forma simples e objetiva.
Confira uma seleção especial de questões comentadas retiradas dos mais diversos concursos públicos realizados pelo Brasil.
Bons estudos.
Questão 1 (PM AC – Funcab). Sabendo que A é uma matriz quadrada de ordem 3 e que o determinante de A é -2, calcule o valor do determinante da matriz 3A.
A) – 8
B) – 54
C) 27
D) 18
E) – 2
Resolução:
Para resolvermos a questão, vamos utilizar uma das propriedades das determinantes:
Onde n é a ordem da matriz quadrada.
Desta propriedade temos que:
Resposta: B
Questão 2 (PM AC – Funcab). Considerando a matriz quadrada A abaixo, e det(A) seu determinante, calcule o valor de 5.det(A).
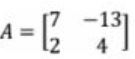
A) 10
B) -140
C) 270
D) 130
E) -35
Resolução:
Calculando o determinante de uma matriz 2×2:
DetA = 7.4 – 2.(-13) = 28 + 26 = 54
Logo,
5.DetA = 5.54 = 270
Resposta: C
Questão 3 (PM PR – Cops). Considere uma colisão de dois veículos. Num sistema de coordenadas cartesianas, as posições finais destes veículos após a colisão são dadas nos pontos A = (2,2) e B = (4, 1). Para compreender como ocorreu a colisão é importante determinar a trajetória retilínea que passa pelos pontos A e B.
Essa trajetória é dada pela equação:
a) x – y = 0
b) x + y – 5 = 0
c) x – 2y + 2 = 0
d) 2x + 2y – 8 = 0
e) x + 2y – 6 = 0
Resolução:
A equação pode ser descoberta calculando o determinante da matriz abaixo, que relaciona os pontos P(x,y), A(2,2) e B(4,1):

Fazendo o produto das diagonais principais menos o produto das diagonais secundárias:
2x + 4y + 2 – 8 – x – 2y = 0
x + 2y – 6 = 0
Resposta: E
Questão 4 (RFB 2009 – Esaf). Com relação ao sistema
onde
pode-se, com certeza, afirmar que:
a) é impossível
b) é indeterminado
c) possui determinante igual a 4
d) possui apenas a solução trivial
e) é homogêneo
Resolução:
Podemos separar a segunda igualdade em duas:
2x – y = 3z + 2 => 2x – y – 3z = 2
2x + y = z + 1 => 2x + y – z = 1
Temos então três equações:
x + y + z = 1
2x – y – 3z = 2
2x + y – z = 1
Que podem ser associadas a matriz:
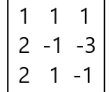
Vamos calcular seu determinante:
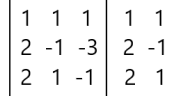
Det = 1.(-1).(-1) + 1.(-3).2 + 1.2.1 – 2.(-1).1 – 1.(-3).1 – (-1).2.1
Det = 1 – 6 + 2 +2 + 3 + 2
Det = 4
Resposta: C
Questão 5 (ANAC – ESAF 2016). Dada a matriz A abaixo, o determinante da matriz 2A é igual a:
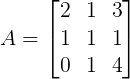
a) 40.
b) 10.
c) 18.
d) 16.
e) 36.
Resolução:
Temos duas formas de resolver a questão. Podemos calcular o determinante da matriz A e depois utilizar a propriedade P3 que se encontra em nosso material didático, ou calcular diretamente o determinante da matriz 2A. Vamos resolvê-la pelo primeiro método, utilizando a regra de Sarrus:
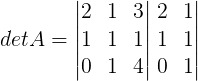
DetA = 2.1.4 + 1.1.0 + 3.1.1 – 0.1.3 – 1.1.2 – 4.1.1
DetA = 8 + 0 + 3 – 0 – 2 – 4
DetA = 5
Utilizando a propriedade citada:
Det2A = 2³.DetA
Det2A = 8.5
Det2A = 40
Resposta: A
Questão 6 (PM ES – AOCP). Para saber o custo total (em reais) na produção de x uniformes para um grupo de soldados, primeiramente substitui-se cada elemento x, da matriz a seguir, pela quantidade de uniformes que se quer produzir e calcula-se o determinante dessa matriz, obtendo-se, assim, o custo total na produção destes x uniformes igual ao valor do determinante.
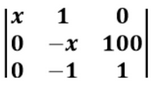
Dessa forma, para se produzir 70 uniformes para um grupo de soldados, o custo total nessa produção será de
(A) R$ 4.100,00.
(B) R$ 3.500,00.
(C) R$ 3.100,00.
(D) R$ 2.500,00.
(E) R$ 2.100,00.
Resolução
Calculando o determinante:
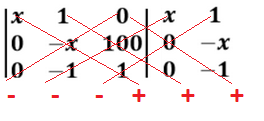
Det = x.(-x).1 + 1.100.0 + 0.0.(-1) – 0.(-x).0 – (-1).100.x – 1.0.1
Det = -x² + 100.x
Quando x = 70, temos:
Det = -70² + 100.70
Det = -4900 + 7000
Det = 2100
Resposta: E
Questão 7 (UP). Considerando a matriz abaixo, qual é o valor de k?
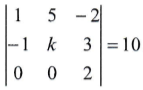
a) 1
b) 2
c) -1
d) 0
Resolução
Temos uma matriz 3×3, cujo determinante pode ser calculado da seguinte forma:
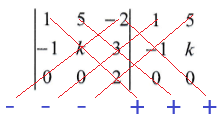
1.k.2 + 5.3.0 + (-2).(-1).0 – 0.k.(-2) – 0.3.1 – 2.(-1).5 = 10
2k + 0 + 0 – 0 – 0 + 10 = 10
2k = 10 – 10
2k = 0
k = 0
Resposta: D
Procurando exercícios resolvidos sobre determinantes?
Deixe o seu comentário.
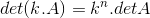
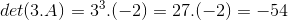
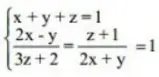
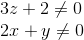
Olá
Parabéns pelo conteúdo, tem me ajudado bastante no concurso da pm que estou estudando. ..
Como que Det = -x² + 100.x virou 70
Pedro,
O objetivo da questão é calcular o custo para 70 uniformes.