Você sabe qual é a derivada da função logarítmica natural (ln)? Veremos agora como é feita a demonstração.
Não deixe de ver também nossas publicações sobre outros tópicos do cálculo diferencial.
Bom estudo!
Como a função natural é um caso especial da função logarítmica, nosso primeiro objetivo será calcular a derivada geral.
Seja a função logarítmica abaixo, de variável x e base a.
![]()
Temos que:
ay = x
Derivando a igualdade implicitamente em relação a x:
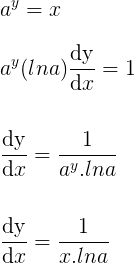
Conclusão:
![]()
Agora que já sabemos qual é a derivada da função logarítmica, podemos calcular facilmente a derivada de lnx. Basta considerarmos a=e.
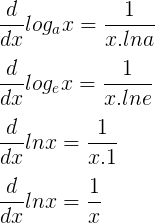
Aprendeu como é feito o cálculo das derivadas?
Deixe o seu comentário.
