Olá amigos estudantes! Nesta página vamos aprender a fazer operações envolvendo matrizes, em especial, vamos aprender como fazer a adição e a subtração de matrizes.
O ideal é que o aluno já tenha acessado o nosso conteúdo introdutório sobre o assunto, onde abordamos a definição e a representação. Caso ainda não tenha acessado, verifique na sessão “material didático”.
Bom estudo!
ADIÇÃO DE MATRIZES
A adição de duas matrizes A e B é muito fácil. Basta somarmos cada um dos elementos correspondentes. A única exigência que devemos respeitar é que ambas devem possuir a mesma quantidade de linhas (m) e a mesma quantidade de colunas (n), ou seja, devem ser da mesma ordem.
O resultado da adição dessas duas matrizes A e B será uma nova matriz C, também m x n.
Vejamos o exemplo:
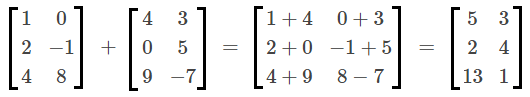
SUBTRAÇÃO DE MATRIZES
Se formos bem rigorosos com os conceitos da matemática, não existe subtração de matrizes. Na verdade, quando representamos a diferença A-B, devemos saber que estamos somando a matriz A com a matriz oposta de B, ou seja, A+(-B). Como na prática isso não vai mudar em nada, vamos considerar que para subtrairmos duas matrizes, basta subtrairmos cada um dos elementos correspondentes.
Lembrando que, assim como na adição, na subtração as matrizes devem possuir a mesma quantidade de linhas e de colunas.
Veja o exemplo:
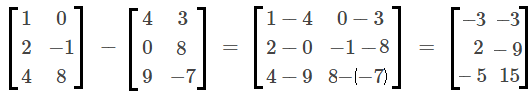
Propriedades da adição de matrizes
Sejam A, B e C matrizes com a mesma quantidade de linhas (m), e a mesma quantidade de colunas (n). Neste caso, as propriedades abaixo são válidas para a adição:
- comutativa: A + B = B + A
- associativa: ( A + B) + C = A + ( B + C).
- elemento neutro: A + 0 = 0 + A = A, onde 0 a matriz nula m x n.
- elemento oposto: A + ( – A) = (-A) + A = 0.
