11) Numa academia militar 38 aspirantes gostam de fazer flexão, 53 gostam de fazer abdominal, 27 gostam das duas modalidades. Nessas condições, o total de aspirantes que gostam de fazer somente uma das duas modalidades é igual a:
a) 118
b) 37
c) 64
d) 91
e) 73
Resolução
Existem 38 que gostam de fazer flexão, 53 que gostam de abdominal e 27 que gostam das duas modalidades.
Podemos calcular a quantidade de aspirantes que gostam de apenas uma modalidade desconsiderando os 27 que gostam de duas modalidades:
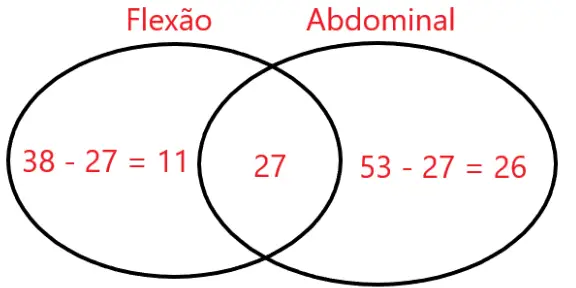
11 gostam apenas de flexão
26 gostam apenas de abdominal
Total: 11 + 26 = 37
Resposta: B
12) De acordo com o Raciocínio Lógico proposicional uma frase que equivale a “Se o oficial faltou ao serviço, então a instrução foi cancelada” é a frase:
a) O oficial não faltou ao serviço ou a instrução foi cancelada
b) O oficial não faltou ao serviço ou a instrução não foi cancelada
c) O oficial faltou ao serviço ou a instrução foi cancelada
d) O oficial faltou ao serviço ou a instrução não foi cancelada
e) O oficial não faltou ao serviço e a instrução foi cancelada
Resolução
Observe que a frase equivale ao condicional P→Q, onde:
P: o oficial faltou ao serviço
Q: a instrução foi cancelada
Para resolvermos a questão, devemos saber que P→Q é equivalente a ~PVQ.
A proposição ~PVQ pode ser escrita da seguinte forma:
O oficial NÃO faltou ao serviço OU a instrução foi cancelada.
Resposta: A
13) As premissas “Se o sargento manteve a disciplina, então o soldado não foi punido”. “Se o soldado não foi punido, então a aula prosseguiu normalmente” implicam na frase:
a) Se o sargento não manteve a disciplina, então a aula prosseguiu normalmente
b) Se o sargento não manteve a disciplina, então a aula não prosseguiu normalmente
c) Se o sargento manteve a disciplina, então a aula prosseguiu normalmente
d) Se o sargento manteve a disciplina, então a aula não prosseguiu normalmente
e) Se a aula prosseguiu normalmente, então o sargento manteve a disciplina
Resolução
Considere que:
P: o sargento manteve a disciplina
Q: o soldado não foi punido
R: a aula prosseguiu normalmente
Neste caso, podemos representar as proposições da seguinte forma:
P→Q: Se o sargento manteve a disciplina, então o soldado não foi punido
Q→R: Se o soldado não foi punido, então a aula prosseguiu normalmente
De P→Q e Q→R, podemos concluir que P→R, que neste caso representa a proposição “Se o sargento manteve a disciplina, então a aula prosseguiu normalmente”.
Resposta: C
14) Sabendo que o valor lógico de uma proposição simples é verdade e o valor lógico de outra proposição é falso, então é correto afirmar que:
a) O valor lógico da disjunção inclusiva entre as duas proposições é falso
b) O valor lógico da conjunção entre as duas proposições é verdade
c) O valor lógico do bicondicional entre as duas proposições é verdade
d) O valor lógico da disjunção exclusiva entre as duas proposições é verdade
e) O valor lógico do condicional entre as duas proposições, em qualquer ordem, é falso
Resolução
Utilizaremos a tabela verdade abaixo para analisarmos cada uma das alternativas.
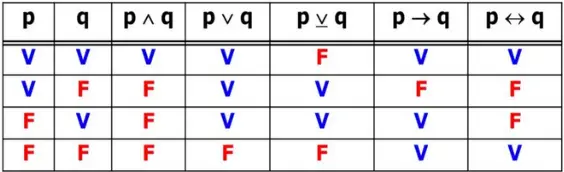
a) A disjunção inclusiva está representada na quarta coluna. Considerando P verdadeiro e Q falso (ou vice-versa), a disjunção inclusiva é verdadeira. ERRADO
b) A conjunção está representada na terceira coluna. Considerando P verdadeiro e Q falso (ou vice-versa), a conjunção é falsa. ERRADO
c) O bicondicional está representado na sétima coluna. Considerando P verdadeiro e Q falso (ou vice-versa), o bicondicional é falso. ERRADO
d) A disjunção exclusiva está representada na quinta coluna. Considerando P verdadeiro e Q falso (ou vice-versa), a disjunção exclusiva é verdadeira. CERTO
e) O condicional está representado na sexta coluna. Considerando P verdadeiro e Q falso, o condicional é falso, porém, considerando Q verdadeiro e P falso, o condicional é verdadeiro. Inconclusivo. ERRADO
Resposta: D
15) O total de proposições simples na frase “O quartel ficou fechado e o feriado foi decretado se, e somente se, o prefeito homologou o dia do soldado ou não foi à festividade”, é igual a:
a) 2
b) 3
c) 5
d) 6
e) 4
Resolução
Observe que temos as seguintes proposições simples:
O quartel ficou fechado
o feriado foi decretado
o prefeito homologou o dia do soldado
o prefeito não foi à festividade
Resposta: E
16) Um conjunto A possui 7 elementos distintos e um conjunto B possui 8 elementos distintos. Nessas circunstâncias é correto afirmar que:
a) Os conjuntos A e B são disjuntos
b) Se o conjunto A tiver 3 elementos em comum com o conjunto B, então a união entre A e B possui 18 elementos distintos
c) Se o conjunto A tiver 5 elementos em comum com o conjunto B, então a união entre A e B possui 10 elementos distintos
d) Se a intersecção entre os conjuntos A e B tiver 3 elementos, então a união entre A e B terá 15 elementos distintos
e) Se a intersecção entre os conjuntos A e B for vazia, então A e B não são disjuntos
Resolução
Analisaremos cada uma das alternativas:
a) Dois conjuntos são considerados disjuntos quando não possuem nenhum elemento em comum. Não podemos afirmar isto pois sabemos apenas a quantidade de elementos de cada um. ERRADO
b) Considerando que eles possuem 3 elementos em comum, podemos calcular a quantidade de elementos da união somando os elementos de cada e subtraindo a quantidade em comum: 7 + 8 – 3 = 12. ERRADO
c) Considerando que eles possuem 5 elementos em comum, podemos calcular a quantidade de elementos da união somando os elementos de cada e subtraindo a quantidade em comum: 7 + 8 – 5 = 10. CERTO
d) Considerando que eles possuem 3 elementos em comum, podemos calcular a quantidade de elementos da união somando os elementos de cada e subtraindo a quantidade em comum: 7 + 8 – 3 = 12. ERRADO
e) Se a intersecção for vazia, então eles SÃO disjuntos. ERRADO
Resposta: C
17) Um capitão deve escolher um grupo de 4 soldados, para fazer uma diligência, dentre 4 homens e 5 mulheres. Se esse grupo for composto por 2 mulheres e 2 homens, então o total de possibilidades de formação desse grupo é igual a:
a) 60
b) 120
c) 240
d) 32
e) 90
Resolução
O capitão deve escolher 2 homens em um grupo de 4, ou seja, podemos calcular a quantidade de possibilidades através de uma combinação de 4, tomados 2 a 2.
C4,2 = 4!/2!2! = 4.3.2.1/2.2 = 6
O capitão deve escolher duas mulheres em um grupo de 5, ou seja, podemos calcular a quantidade de possibilidades através de uma combinação de 5, tomados 2 a 2.
C5,2 = 5!/3!2! = 5.4.3.2.1/3.2.2 = 10
O número de possibilidades do grupo de 4 soldados pode ser calculado através do produto:
6 x 10 = 60
Resposta: A
18) Para se comunicar com seus subordinados, um tenente criou uma senha formada por 3 números diferentes, sendo que o primeiro número não pode ser par. Nessas condições, a probabilidade de essa senha ser o número 745, é:
a) 1/400
b) 1/500
c) 1/420
d) 1/360
e) 1/450
ANULADA
19) De acordo com a lógica proposicional a negação da frase “O soldado prestou continência e o major retribuiu” deve ser a frase:
a) O soldado não prestou continência e o major não retribuiu
b) O soldado não prestou continência ou o major retribuiu
c) O soldado prestou continência ou o major não retribuiu
d) O major não retribuiu e o soldado não prestou continência
e) O soldado não prestou continência ou o major não retribuiu
Resolução
Temos uma conjunção, que pode ser representada da seguinte forma:
P^Q, onde:
P: O soldado prestou continência
Q: o major retribuiu
A negação da conjunção é:
~ (P^Q) = ~PV~Q
~PV~Q: O soldado não prestou continência ou o major não retribuiu.
Resposta: E
20) De acordo com o Raciocínio Lógico proposicional, dentre as frases descritas abaixo, a única que não pode ser considerada uma proposição, é:
a) O Sol é um planeta
b) Choverá amanhã
c) 3 + 5 = 8
d) A capital de Florianópolis é Santa Catarina
e) 25 de agosto é considerado “Dia do soldado”
Resolução
Proposição é uma frase declarativa que pode assumir um dos valores lógicos “verdadeiro” ou “falso”, sem ambiguidade.
Observe que a única que não possui essas características é a frase localizada na letra B, que está se referindo ao futuro, ou seja, ainda não é possível classificar como V ou F.
Resposta: B
Gostou da prova resolvida do concurso para a Polícia Militar do Estado do Rio Grande do Norte de 2023 (PM RN 2023)? A prova foi elaborada pela IBFC para o cargo de soldado.
