Dando continuidade ao estudo das funções, veremos aqui o Teorema do Valor Intermediário, onde apresentaremos o teorema e alguns exemplos de aplicação.

Não deixe de ver também as nossas publicações sobre os outros tópicos do cálculo numérico.

Bom estudo!

Teorema do valor intermediário. Seja f uma função contínua no intervalo [a, b]. Se existe y₀, tal que f(a) ≤ y₀ ≤ f(b), ou f(b) ≤ y₀ ≤ f(a), então existe x₀ tal que f(x₀) = y₀.

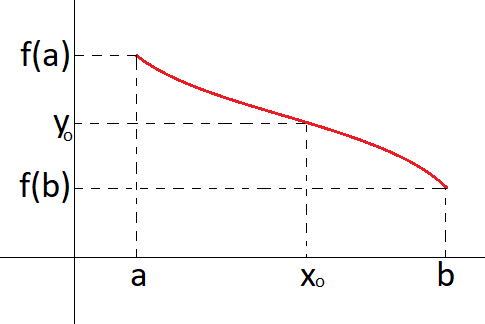
Observações importantes:

• A função precisa ser necessariamente contínua no intervalo [a, b];
• Não importa se f(a) é maior ou menor que f(b), o teorema vale quando y₀ está entre f(a) e f(b);
• Se f(a) = f(b), a única opção é y₀ = f(a), bastando tomar, por exemplo, x₀ = a para que o teorema seja válido.

APLICAÇÕES

Exemplo. Demonstrar que a equação x³ + 3x² – 5 = 0 possui pelo menos uma raiz real.

Devemos analisar a função f(x) = x³ + 3x² – 5, que por ser polinomial, é uma função contínua.

Temos:

f(1) = 1³ + 3.1² – 5 = 1 + 3 – 5 = -1

f(2) = 2³ + 3.2² – 5 = 8 + 12 – 5 = 15

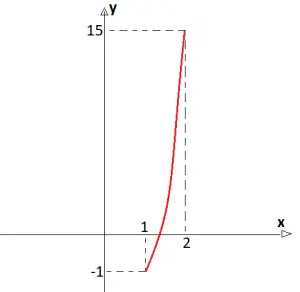
Pelo Teorema do Valor Intermediário, podemos concluir que existe x₀∈[1,2], tal que f(x_o) = 0, de onde podemos concluir que a equação x³ + 3x² – 5 = 0 possui pelo menos uma raiz real.

Gostou da nossa publicação sobre o Teorema do Valor Médio?

Deixe o seu comentário.