Buscando exercícios resolvidos sobre média, moda e mediana? Aqui você encontra questões de concursos públicos realizados por todo o país, de diversas bancas e níveis.
Os concursos que exigem dos inscritos conhecimento sobre estatística de nível superior estão entre os mais difíceis e concorridos. Por isso é muito importante dominar os conteúdos introdutórios como média, moda e mediana.
Comece já a estudar e saia na frente.
Bons estudos!
Questão 1 (TJ SP 2014 – Vunesp). Certa competição tem 6 etapas eliminatórias. Sabe-se que a média aritmética do número de pessoas que participaram da primeira e da segunda etapa é igual ao quádruplo da média aritmética do número de pessoas que participaram de cada uma das quatro etapas seguintes.
Desse modo, a razão entre o número de pessoas que participaram da primeira e da segunda etapa e o número total de pessoas que participaram dessa competição é de
a) 1/2
b) 1/3
c) 1/4
d) 2/3
e) 3/4
Resolução:
Vamos representar cada etapa pelas letras a, b, c, d, e, f, nesta ordem.
Utilizando o conceito de média aritmética, temos pelo enunciado que:
(a + b)/2 = 4.(c + d + e + f)/4
(a + b)/2 = (c + d + e + f)
Somando (a + b) em ambos os lados temos:
(a + b)/2 + (a + b) = (c + d + e + f) + (a + b)
(a + b)/2 + 2(a + b)/2 = (a + b + c + d + e + f)
(a + b)3/2 = (a + b + c + d + e + f)
(a + b) = (a + b + c + d + e + f)2/3
Logo, a quantidade de participantes das duas primeiras etapas representa 2/3 do total.
Resposta: D
Clique aqui para assistir a resolução no youtube.
Questão 2 (BB 2013 – Fundação Carlos Chagas). Nos quatro primeiros dias úteis de uma semana o gerente de uma agência bancária atendeu 19, 15, 17 e 21 clientes. No quinto dia útil dessa semana esse gerente atendeu n clientes. Se a média do número diário de clientes atendidos por esse gerente nos cinco dias úteis dessa semana foi 19, a mediana foi
(A) 21.
(B) 19.
(C) 18.
(D) 20.
(E) 23.
Resolução:
Para calcularmos a média aritmética, somamos os valores e dividimos pela quantidade de termos:
Média = (19 + 15 + 17 + 21 + n) / 5 = 19
19 + 15 + 17 + 21 + n = 19 x 5
72 + n = 95
n= 95 – 72 = 23
Nossa sequencia ordenada é então: 15, 17, 19, 21, 23
Como a mediana é o termo do meio quando ordenados, a resposta é 19.
Resposta: B
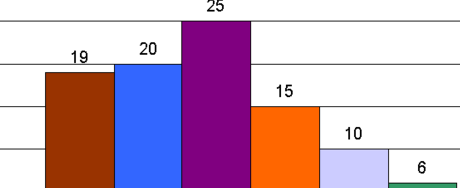
Questão 3 (PM ES 2013 – Exatus). A tabela que segue é demonstrativa do levantamento realizado por determinado batalhão de Polícia Militar, no que se refere às idades dos policiais integrantes do grupo especial desse batalhão:
Idade Nr. de Policiais
25 12
28 15
30 25
33 15
35 10
40 8
A moda, média e mediana dessa distribuição são, respectivamente, iguais a:
a) 30, 31, 30
b) 30, 31, 31
c) 30, 30, 31
d) 31, 30, 31
e) 31, 31, 30
Resolução:
Moda é o valor que aparece com mais frequência: 30.
Média: Temos que somar todas as idades e dividir pela quantidade de policiais:
(25×12 + 28×15 + 30×25 + 33×15 + 35×10 + 40×8)/85
= (300 + 420 + 750 + 495 + 350 + 320)/85
= 2635/85 = 31
Mediana é o termo do meio quando colocamos todos em ordem:
São 85 termos, o do meio é o termo de número 43, ou seja, 30 anos.
Resposta: A
Questão 4 (Prova Resolvida PM ES 2013 – Funcab). A tabela abaixo representa os dados dos balanços das operações do Batalhão de Polícia de Trânsito (BPTran) da Polícia Militar – ES em três grandes feriados nacionais do ano de 2012.
Dia do trabalho: 220 acidentes, 2 mortos, 78 feridos
Dia de finados: 186 acidentes, 2 mortos, 54 feridos
Dia do trabalho: 219 acidentes, 1 mortos, 51 feridos
O valor que melhor representa a média do número de feridos, de acordo com a tabela acima, é:
A) 57
B) 59
C) 61
D) 63
E) 65
Resolução:
Calculando a média aritmética:
(78 + 54 + 51)/3 = 183/3 = 61
Resposta: C
Questão 5 (Prova Resolvida Sejus ES 2013 – Vunesp). A média aritmética dos salários de 4 funcionários de uma empresa é R$ 2.500,00. A média aritmética dos salários dos dois primeiros é R$ 3.000,00, o quarto ganha R$ 500,00 a mais que o terceiro. Nesse caso, o salário do quarto empregado é igual a
(A) R$ 2.350,00.
(B) R$ 2.750,00.
(C) R$ 2.520,00.
(D) R$ 2.250,00.
(E) R$ 3.250,00.
Resolução:
Vamos chamar de x, y, z, w o salário de cada funcionários.
Como a média dos salários dos 4 é 2500:
(x + y + z + w)/4 = 2500
x + y + z + w = 4.2500
x + y + z + w = 10000 (1)
Como a média dos salários dos dois primeiros é 3000:
(x + y)/2 = 3000
x + y = 2.3000
x + y = 6000 (2)
Como o quarto ganha 500 a mais que o terceiro:
w – z = 500 (3)
Fazendo (1) – (2):
z + w = 4000 (4)
Fazendo (3) + (4):
2w = 4500
w = 4500/2 = 2250
Resposta: D
Questão 6 (Prova Resolvida PM SP 2012). João tem 5 filhos, sendo que dois deles são gêmeos. A média das idades deles é 8,6 anos. Porém, se não forem contadas as idades dos gêmeos, a média dos demais passa a ser de 9 anos. Pode-se concluir que a idade dos gêmeos, em anos, é
(A) 6,5.
(B) 7,0.
(C) 7,5.
(D) 8,0.
(E) 8,5.
Resolução:
Seja x a idade de cada um dos gêmeos.
Como a média das idades dos 3 filhos que não são gêmeos é 9, a soma das idades dos 3 é 27 anos.
Sabendo que a média dos 5 filhos é 8,6 temos:
(27 + 2x)/5 = 8,6
27 + 2x = 8,6.5
2x = 43 – 27
2x = 16
x = 16/2
x = 8 anos
Resposta: D
Clique aqui para assistir a resolução no YouTube.
Questão 7 (Prova Resolvida RFB 2009 – Esaf). Considere a seguinte amostra aleatória das idades em anos completos dos alunos em um curso preparatório. Com relação a essa amostra, marque a única opção correta:
29, 27, 25, 39, 29, 27, 41, 31, 25, 33, 27, 25, 25, 23, 27, 27, 32, 26, 24, 36, 32, 26, 28, 24, 28, 27, 24, 26, 30, 26, 35, 26, 28, 34, 29, 23, 28.
a) A média e a mediana das idades são iguais a 27.
b) A moda e a média das idades são iguais a 27.
c) A mediana das idades é 27 e a média é 26,08.
d) A média das idades é 27 e o desvio-padrão é 1,074.
e) A moda e a mediana das idades são iguais a 27.
Resolução:
Primeiramente vamos colocar as 37 idades em ordem crescente:
23, 23, 24, 24, 24, 25, 25, 25, 25, 26, 26, 26, 26, 26, 27, 27, 27, 27, 27, 27, 28, 28, 28, 28, 29, 29, 29, 30, 31, 32, 32, 33, 34, 35, 36, 39, 41.
A moda é o valor que aparece com mais frequência. Note que o 27 aparece 6 vezes e nenhum outro aparece com tanta frequência.
A mediana é o valor que, após ordenar todos os valores, se encontra no centro. Note que o 27 se encontra na posição 19º, ou seja, exatamente no meio.
Resposta: E
Questão 8 (Prova Resolvida PRF 2008 – Cespe). Ficou pior para quem bebe. O governo ainda espera a consolidação dos dados do primeiro mês de aplicação da Lei Seca para avaliar seu impacto sobre a cassação de CNHs. As primeiras projeções indicam, porém, que as apreensões subirão, no mínimo, 10%.
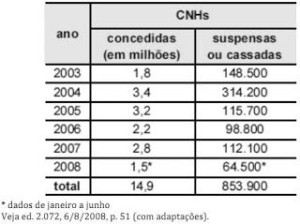
Antes da vigência da Lei Seca, eram suspensas ou cassadas, em média, aproximadamente 155.000 CNHs por ano. Se as previsões estiverem corretas, a média anual deve subir para próximo de 170.000. A tabela a seguir mostra esses resultados nos últimos anos( fonte: DENATRAN ).
Para que a média de CNHs suspensas ou cassadas, de 2003 a 2008, atinja o valor previsto de 170.000, será necessário que, em 2008, a quantidade de CNHs suspensas ou cassadas seja um número
A) inferior a 180.000.
B) superior a 180.000 e inferior a 200.000.
C) superior a 200.000 e inferior a 220.000.
D) superior a 220.000 e inferior a 240.000.
E) superior a 240.000
Resolução:
Para fazer a média dos 6 anos, devemos observar que em 2008 temos dados até junho. Vamos chamar de x o número de CNH cassadas ou suspensas de julho a dezembro e calcular a média:
(853900 + x) / 6 = 170000
853900 + x = 6.170000
853900 + x = 1020000
x = 1020000 – 853900 = 166100
Logo, 166100 + 64500 = 230600
Resposta: D
Questão 9 (Prova Resolvida Caixa 2006 – Cespe). A CAIXA criou as Cestas de Serviços com o compromisso de valorizar o relacionamento com seus clientes e oferecer cada vez mais vantagens.
Você paga apenas uma tarifa mensal e tem acesso aos produtos e serviços bancários que mais se adequarem ao seu relacionamento com a CAIXA.
Alguns dos itens disponíveis têm seu uso limitado. Caso você exceda as quantidades especificadas ou utilize um item não incluso na sua cesta, será cobrado o valor daquele 10 produto ou serviço discriminado na Tabela de Tarifas vigente.
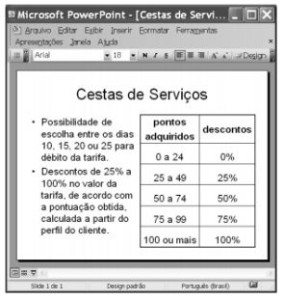
A janela do PowerPoint 2003 a seguir apresenta, no slide em edição, outras informações acerca das Cestas de Serviços da CAIXA.
Com base nas informações do texto e sabendo que, a cada R$ 100,00 de saldo médio no trimestre em aplicação na poupança, o cliente acumula 1 ponto para o cálculo do desconto na tarifa mensal de serviços, julgue os seguintes itens.
Considere a seguinte situação hipotética.
Carlos, cliente da CAIXA, obteve exatamente 5 pontos relativos ao saldo médio de suas aplicações em poupança no primeiro trimestre de 2006.
Julgue a seguinte afirmação:
“Nessa situação, para dobrar essa pontuação no trimestre seguinte, caso não faça retiradas ao longo desse período, é necessário que Carlos deposite a quantia de R$ 500,00 em sua conta poupança no início de cada mês do segundo trimestre.”
ERRADO
Para que Carlos dobre sua pontuação, ele deve possuir R$ 1.000,00 de saldo médio. Note que os R$ 500,00 não serão retirados, logo as aplicações futuras devem gerar mais R$ 500,00 de saldo médio.
Pelo questão ele deve depositar R$ 500,00 durante 3 meses. Veja:
Mês 1 = Saldo 500
Mês 2 = Saldo 1000
Mês 3 = Saldo 1500
Média = 1000, que somados aos 500 que ele já tinha, são 1500.
oi Jordon, tudo bem?kkkkkkk muito bom seu site, estou dando uma olha em media moda e mediana…. você é o cara.
Valeu Kamila rsrsrs
volte sempre…
voces teem certeza que as contas estao corretas estou aparentemente vendo erro na questao 78 gostaria que voces revisassem
Lucas,
aparentemente a questão está correta.
Caso identifique o erro nos informe.
Olá.
Sobre a questão 78 eu não entendi o resultado da mediana é 30. Poderia explicar?
Olá Rosiane,
Se você ordenar todas as idades, a do meio será 30 anos.
Boa tarde! Mas a mediana quando se tem uma quantidade par de números, se calcila os 2 do meio. Soma e divide por dois. Ou estou enganada.
Isabelle, realmente você está correta, porém em nosso exercício, a quantidade de policiais é 85, ou seja, ímpar.
Jordon, voçê teria exercicios resolvidos de frequência relativa e absoluta ?
Olá Lais,
Eu ainda não fiz uma página sobre o assunto pois até hoje não resolvi muitas provas com essas questões. Vou tentar publicar alguma coisa para você.
Boa Noite.
Como calculo a MODA quando a Classe Modal posterior nao existe ?
como calculo a mediana?
Olá Nildo,
A mediana é o número que se encontra exatamente no meio quando colocamos todos em ordem.
Exemplo:
A mediana dos números 1, 2, 3, 10, 105 é 3
vc é um lokooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooocuoooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooooo
Olá Nildo,
A mediana é o número que se encontra exatamente no meio quando colocamos todos em ordem.
Exemplo:
A mediana dos números 1, 2, 3, 10, 105 é 3
Oi, não entendi pq na questão 78 dos policiais em relação a mediana, o termo de número 43 é equivalente a 30 anos
Joyce,
A questão informa que são 85 policiais. Se fizermos uma fila em ordem crescente de idade, o policial do meio terá 30 anos.
como a resposta é 30 se tem os números são pares??? só eu que vi isso?
17) O quadro abaixo apresenta a distribuição de notas em
uma turma de 7º Ano do Ensino Fundamental:
Número de
alunos………..Nota
3………………..9
5………………..7
12………………6
4………………..5
Com base nesse quadro, é CORRETO afirmar que:
a) A metade da turma tirou nota maior que 6.
b) A nota média da turma foi 7.
c) Aproximadamente 67% da turma tirou 6 ou menos.
d) Cerca de 35% da turma tirou uma mesma nota.
Quql a resposta correta?
Letra C) Aproximadamente 67% da ruema tirou 6 ou menos.
Visto que a turma tem um total de 24 alunos, considerando que 12 alunos que tiraram nota 6 representam 50% da turma e 4 alunos que tiraram nota 5 representam 16,6% da turma, podemos concluir que 66,6% da turma tiraram uma nota igual ou inferior a 6.
Letra A) ^^
É a letra C)
Me Desculpe ._.
muito bom e me ajudo bastante.
Olá, muuuuuuuuuuuito obrigada me salvo de um trabalho de matemática, salva da escola adeeeus terceirão <3 uehuehueh ;*
Obrigado Cibelle,
Volte sempre.
Parabéns pelos exercícios e a forma como responde cada questionamento.
Poucos sites o administrador dar tanta atenção ao visitante. Você é um ótimo administrador Jordon
Obrigado Thaise.
Volte sempre!
Jordon
OLA jORDAN, NA QUESTÃO DOS POLICIAIS, PODERIA EXPLICAR MAIS DETALHADO A MEDIANA?
Oi Bruna,
O que você não entendeu especificamente?
muito bom.
Parabéns pelo trabalho! Preparando-me para o CFO 2016 PMSP.
Eu não entendi na questão 78 por que a mediana é 30, me explica?
Ah,já entendi
PARABÉNS JORDON.
A QUESTÃO 8 TROUXE UM VALOR NA TABELA ERRADO. O NÚMERO DE CARTEIRAS SUSPENSAS OU CASSADAS É 853800 E NÃO 853900.
Olá professor. Desculpe mas não identifiquei o erro. A tabela apresenta o número 853900.
Na questão 8, a soma é 853800 e não 853900 (como está na tabela).
Obrigado Iranildo!
Não alterarei a resolução pois a tabela foi retirada diretamente do caderno de questões.
Parabéns Jordon!! Seu trabalho é muito proveitoso. Obrigada
Parabéns Jordon!! Seu trabalho é muito proveitoso
Parabéns Jordon!! Seu trabalho é muito proveitoso
obrigada jordon!!! você me salvou na prova de matemática (tirei 10), continui assim, você vai poder ajudar varias outras pessoas.
Jordon obrigado por ser tão paciente…
Muito bom os exercícios. .
O que quer dizer 0,2 em aritmética de 23?