Procurando exercícios resolvidos sobre progressão aritmética, a famosa PA? Chegou ao site certo.
Confira uma lista especial de questões comentadas, todas retiradas de diversos concursos públicos realizados pelo país.
Bons estudos.
Questão 1 (CFO PM ES – Exatus). Numa cerimônia militar, os soldados de um quartel da capital capixaba foram organizados em fileiras. Na primeira fileira havia 18 soldados, na segunda 20 soldados, na terceira 22 soldados e assim sucessivamente. Sabe-se que no total havia 480 soldados nessa cerimônia. Qual o número de fileiras de soldados que foram formadas nessa cerimônia?
a) 15
b) 16
c) 17
d) 18
e) 19
Resolução
Nota-se que temos uma Progressão Aritmética, onde o primeiro termo é o 18, a razão é o 2 e a soma dos termos é 480.
Pela fórmula do termo geral:
an = a1 + (n – 1)r
an = 18 + (n – 1)2
an = 18 + 2n – 2
an = 16 + 2n
Vamos agora substituir na fórmula da soma dos termos de uma P.A.
Sn = (a1 + an).n/2
480 = (18 + 16 + 2n).n/2
480.2 = (34 + 2n)n
960 = 34n + 2n²
2n² + 34n – 960 = 0
n² + 17n – 480 = 0
Temos uma equação do segundo grau.
Resolvendo pelo método de soma e produto:
Soma = -b/a = -17
Produto = c/a = -480
Os dois números cuja soma é -17 e o produto é -480 são -32 e 15.
Como o n representa a quantidade de termos, os valores negativos não servem, logo, n = 15.
Resposta: A
Questão 2 (PM ES – Exatus). O comandante de um destacamento militar ordenou que seus subordinados se organizassem em filas. A primeira fila era composta por 14 soldados, a segunda por 18 soldados, a terceira por 22 soldados, e assim sucessivamente. Sabe-se que o número de soldados deste destacamento é igual a 1550. Dessa forma, é correto afirmar que serão formadas:
a) 18 filas
b) 20 filas
c) 23 filas
d) 25 filas
e) 30 filas
Resolução
Temos uma Progressão Aritmética, onde:
a1 = 14
r = 4
Sn = 1550
Precisamos descobrir o valor de n (número de termos)
Pela fórmula do termo geral:
an = a1 + (n – 1)r
an = 14 + (n – 1)4
an = 14 + 4n – 4
an = 4n + 10
Pela fórmula da soma dos termos:
Sn = (a1 + an)n/2
1550 = (14 + an)n/2
Vamos substituir an = 4n + 10 na segunda expressão:
1550 = (14 + 4n + 10)n/2
2.1550 = (4n + 24)n
3100 = 4n² + 24n
4n² + 24n – 3100 = 0
n² + 6n – 775 = 0
Δ = b² – 4ac
Δ = 6² – 4.1.(-775)
Δ = 36 +3100
Δ = 3136
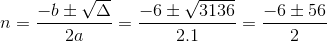
Assim,
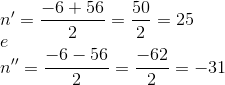
Como n representa o número de filas, vamos considerar apenas o valor positivo.
Resposta: D
Questão 3 (PM SC – Cesiep). Certo cometa foi visível da Terra por alguns dias nos anos de 1774, 1787, 1800, etc., tendo sempre mantido essa regularidade. A próxima aparição deste cometa ocorrerá novamente no ano de:
a) 2020
b) 2023
c) 2019
d) 2021
Resolução
Nota-se que o cometa aparece a cada 13 anos.
Considerando que estamos em 2013 e que o cometa passou em 1800:
2013 – 1800 = 213
2013 dividido por 13 é 16 e sobra 5, logo, precisamos de mais 8 anos para a próxima passagem do cometa:
2013 + 8 = 2021
Resposta: D
Questão 4 (CFO ES Bombeiros – Cespe). As distâncias entre 3 cidades, medidas em quilômetros, são os comprimentos dos lados de um triângulo retângulo. Considerando que essas medidas estão em progressão aritmética, com razão 45, julgue os itens a e b.
a) A menor distância entre as 3 cidades é inferior a 130 km.
b) A soma das distâncias entre as 3 cidades é igual a 540 km.
Resolução:
Se estão em P.A. de razão 45, temos:
hipotenusa = x + 45
cateto 1 = x
cateto 2 = x – 45
Usando o Teorema de Pitágoras
(x + 45)² = x² + (x – 45)²
x² + 90x + 45² = x² + x² – 90x + 45² (“cortando” x² e 45² que se repetem)
0 = x² – 90x – 90x
x² – 180x = 0
x(x – 180) = 0
Daí, x = 0 ou x = 180
Vamos descartar x = 0 pois trata-se de um dos lados do triângulo.
Cada lado medirá: 225 (180 + 45), 180 e 135 (180 – 45)
a) A menor distância entre as 3 cidades é inferior a 130 km.
A menor distância é 135 km
ERRADO
b) A soma das distâncias entre as 3 cidades é igual a 540 km.
225 + 180 + 135 = 540 km
CERTO
Questão 5 (BB – Cesgranrio). Segundo dados do Instituto Internacional de Pesquisa da Paz de Estocolmo (Simpri), os gastos militares dos Estados Unidos vêm crescendo nos últimos anos, passando de 528,7 bilhões de dólares, em 2006, para 606,4 bilhões de dólares, em 2009. Considerando que este aumento anual venha acontecendo de forma linear, formando uma progressão aritmética, qual será, em bilhões de dólares, o gasto militar dos Estados Unidos em 2010?
(A) 612,5
(B) 621,3
(C) 632,3
(D) 658,5
(E) 684,1
Resolução
Lembrando que em uma P.A. o aumento é sempre o mesmo, e esse aumento é chamado de razão da P.A.
Vamos calcular o aumento, em bilhões de dólares, de 2006 a 2009:
606,4 – 528,7 = 77,7
Como o aumento foi em 3 anos, a cada ano os gastos cresceram 25,9 bilhões.
Assim, em 2010 dos gastos foram de:
606,4 + 25,9 = 632,3 bilhões
Resposta: C
Questão 6 (PM Paraná – Cops). Três números estão em uma progressão aritmética (PA) crescente. O produto dos três é 66 e a soma deles é 18. Determine o próximo termo dessa progressão aritmética.
a) a4 = 12
b) a4 = 13
c) a4 = 14
d) a4 = 15
e) a4 = 16
Resolução
Observe que podemos representar os três números por x-r, x, x+r, onde r = razão. Temos:
x – r + x + x + r = 18
3x = 18
x = 18/3
x = 6
(x – r).x.(x + r) = 66
(6 – r).6(6 + r) = 66
(36 – r²).6 = 66
216 – 6r² = 66
6r² = 216 – 66
6r² = 150
r² = 150/6 = 25
r = 5
Logo,
a3 = 6 + 5 = 11
a4 = 11 + 5 = 16
Resposta: E
Questão 7 (INSS – Cespe) A tabela abaixo mostra, em porcentagens, a distribuição relativa da população brasileira por grupos etários, de acordo com dados dos censos demográficos de 1940 a 2000.

Com base nos dados acerca da evolução da população brasileira apresentados na tabela acima, julgue a afirmação abaixo:
“De acordo com os dados apresentados na tabela, os percentuais relativos à população brasileira com idade entre 15 e 64 anos formam uma progressão aritmética de razão menor que 1.”
Resolução
Temos a sequência: 54,9; 55,6; 54,6;…
Note que já nos primeiros termos não existe um padrão, ou seja, nem pode ser considerada uma P.A.
Resposta: Errado
Questão 8 (PRF – Cespe). O governo ainda espera a consolidação dos dados do primeiro mês de aplicação da Lei Seca para avaliar seu impacto sobre a cassação de CNHs. As primeiras projeções indicam, porém, que as apreensões subirão, no mínimo, 10%. Antes da vigência da Lei Seca, eram suspensas ou cassadas, em média, aproximadamente 155.000 CNHs por ano. Se as previsões estiverem corretas, a média anual deve subir para próximo de 170.000. A tabela a seguir mostra esses resultados nos últimos anos( fonte: DENATRAN ).
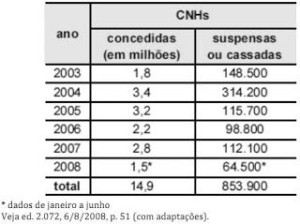
Supondo que, neste ano de 2008, a variação na quantidade de CNHs emitidas de um mês para o mês anterior seja mantida constante e que, em fevereiro de 2008, tenham sido emitidas 175.000 habilitações, então o total de habilitações emitidas em 2008 será, em milhões,
A) inferior a 3.
B) superior a 3 e inferior a 3,5.
C) superior a 3,5 e inferior a 4.
D) superior a 4 e inferior a 4,5.
E) superior a 4,5.
Resolução:
Como a variação é constante, vamos assumir que a cada mês aumenta x, e como em fevereiro foram emitidas 175000 habilitações, temos:
(175000 – x) + (175000) + (175000 + x) + (175000 + 2x) + (175000 + 3x) + (175000 + 4x) = 1500000
1050000 + 9x = 1500000
9x = 450000
x = 50000
Veja que temos uma Progressão Aritmética: 125000, 175000, 225000, …
a12 = 125000 + 11.50000 = 675000
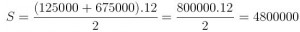
Resposta: E
Questão 9 (Caixa – Cespe). A CAIXA criou as Cestas de Serviços com o compromisso de valorizar o relacionamento com seus clientes e oferecer cada vez mais vantagens.
Você paga apenas uma tarifa mensal e tem acesso aos produtos e serviços bancários que mais se adequarem ao seu relacionamento com a CAIXA.
Alguns dos itens disponíveis têm seu uso limitado. Caso você exceda as quantidades especificadas ou utilize um item não incluso na sua cesta, será cobrado o valor daquele 10 produto ou serviço discriminado na Tabela de Tarifas vigente.
A janela do PowerPoint 2003 a seguir apresenta, no slide em edição, outras informações acerca das Cestas de Serviços da CAIXA.
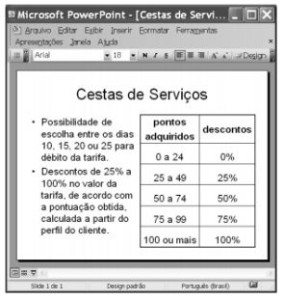
Com base nas informações do texto e sabendo que, a cada R$ 100,00 de saldo médio no trimestre em aplicação na poupança, o cliente acumula 1 ponto para o cálculo do desconto na tarifa mensal de serviços, julgue a seguinte afirmação:
“A sequência numérica formada pelos dias que podem ser escolhidos para débito da tarifa constitui uma progressão aritmética cuja razão é um número racional”.
Resolução
O cliente pode escolher entre os dias: 10, 15, 20 e 25.
Nota-se que os quatro números formam uma PA de razão 5, que claramente é um número racional.
Resposta: Certo
Questão 10. Os bancos oferecem algumas alternativas de financiamento e amortização de dívidas. O sistema de amortização é que define a forma de cálculo da prestação. Os sistemas atualmente praticados pelas instituições financeiras incluem: sistema de amortização constante (SAC) e sistema francês de amortização (Tabela Price).
Suponha que Paulo conseguiu financiar, pelo sistema francês de amortização, um microcomputador no valor de R$ 5.000,00, em doze parcelas mensais e iguais, com taxa de juros de 5% ao mês, com o 1.º pagamento feito 30 dias após a assinatura do contrato. A figura a seguir apresenta uma janela do Excel 2003 contendo a planilha do financiamento obtido por Paulo. O conteúdo das células D9 e E10 está formatado para a cor da fonte branca. Os valores correspondentes a “prestação”, “juros”, “amortização”, “saldo devedor” e “totais” foram calculados utilizando-se o Excel 2003, com as células formatadas para número com duas casas decimais, o que ocasiona arredondamento para cima quando o algarismo da terceira casa decimal é maior ou igual a 5.

A partir das informações acima, julgue o item a.
a) O SAC consiste em um sistema de amortização de dívida em prestações periódicas, sucessivas e em progressão geométrica decrescente, ou seja, com razão menor que 1, no qual o valor da prestação é composto por uma parcela de juros uniformemente decrescente e outra de amortização, que permanece constante ao longo de todo o período do
financiamento.
ERRADO
No SAC as prestações são apresentadas na forma de PA e não de PG, como afirma a questão.
Questão 11. Observe a sequência de figuras com bolinhas.
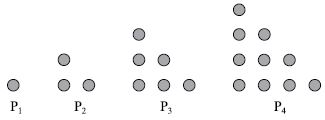
Mantendo-se essa lei de formação, o número de bolinhas na 13.a posição (P13) será de
(A) 91.
(B) 74.
(C) 63.
(D) 58.
(E) 89.
Resolução
Repare que:
P1 = 1
P2 = 1 + 2
P3 = 1 + 2 + 3
…
P13 = 1 + 2 + 3 + … + 12 + 13
Basta somarmos os termos dessa PA, onde a1 = 1, a13 = 13 e n = 13
Pela fórmula da soma de uma PA:
Sn = (a1 + an).n/2
S13 = (1 + 13). 13/2
S13 = 14.13/2
S13 = 91
Resposta: A
Clique aqui para ver o nosso vídeo com exercícios resolvidos sobre progressão aritmética.
Questão 12 (PM PE – IAUPE). Foram abertas 18 turmas de um novo curso que ocorrerá em três turnos. A quantidade de turmas disponíveis para tarde, manhã e noite segue, nessa ordem, uma progressão aritmética de razão 4.
Quantas turmas serão formadas para o turno da noite?
a) 8
b) 10
c) 6
d) 2
e) 12
Resolução
Como as quantidades de turmas nos três turnos estão ordenadas como uma progressão aritmética de razão 4, temos:
Tarde: x – 4
Manhã: x
Noite: x + 4
Sabendo que foram abertas 18 turmas, temos:
x – 4 + x + x + 4 = 18
3x = 18
x = 18/3
x = 6
Total de turmas:
Tarde: x – 4 = 2
Manhã: x = 6
Noite: x + 4 = 10
Resposta: B
Gostou dos nossos exercícios resolvidos sobre progressão aritmética?
Deixe o seu comentário.
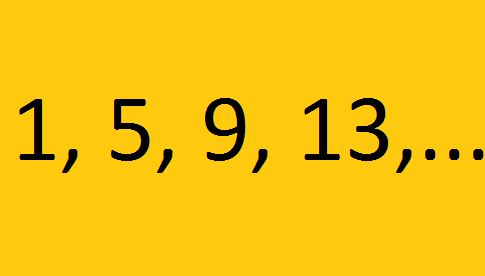
bom dia, eu me chamo Daniel, queria saber o porque da questão 2 quando em sua resposta está na equação de 2 grau você divide toda a equação por 4, assim alterando o resultado da PA, queria só conseguir entender porque você simplificou dessa form alterando o resultado.
Olá Daniel,
Quando dividimos uma equação do segundo grau por um número real as raízes não se alteram.
Se o primeiro termo de uma PÁ for 1 e o quinto termo for 9,qual o valor da razão dessa progressao???
Olá Catiane,
1-3-5-7-9
Razão 2.
Se o primeiro termo de uma PÁ for 2 e o quinto e o último termo dessa PÁ for 100 qual será a soma total dos seus termos?
Alguém me ajude nessas questões urgente
Se o primeiro termo de uma PÁ for 1 e o quinto termo for 9,qual o valor da razão dessa progressao???
Alguém pode por gentileza me ajudar
Oi Professor , porque na questão 3 ( cometa) a diferença foi realizada a diferença: 2013-1800 e não 2013-1774? Grato pela atenção ,seu blog é muito bom,parabéns.
Hélio,
Observe que pelo raciocínio utilizado, pouco importa 1800 ou 1774, pois o importante aqui é o resto, que será sempre o mesmo.
Boa noite,
Será que poderia solucionar este questão de PA ?
1 – Em uma progressão aritmética, a soma do 4° termo com o 7° termo é 41. Qual a soma dos 10 primeiros termos ?
Grato pela ajuda no problema