Confira aqui vários exercícios resolvidos sobre probabilidade, todos retirados dos últimos concursos públicos realizados pelo país.
O ideal é que o estudante leia primeiro o nosso conteúdo sobre o assunto e também sobre análise combinatória.
Bom estudo.
Questão 1 (BNB – FGV). Pedro pergunta a Paulo se ele pode trocar uma nota de R$ 100,00 por duas notas de R$ 50,00. Paulo responde que tem exatamente R$ 200,00 na carteira em notas de R$ 50,00, R$ 20,00 e R$ 10,00, mas não sabe quantas notas tem de cada valor. Sabe apenas que tem pelo menos uma de cada valor. Considere que todas as distribuições possíveis de notas de R$50,00, R$20,00 e R$10,00 que podem ocorrer na carteira de Paulo sejam igualmente prováveis. A probabilidade de que Paulo possa fazer a troca pedida por Pedro é de:
a) 2/13
b) 4/13
c) 5/13
d) 6/13
e) 7/13
Resolução
Sabemos que para calcular probabilidade, basta dividirmos o número de casos favoráveis pelo número de casos possíveis.
Como ele tem pelo menos uma nota de cada, então ele consegue formar 80,00 com uma de 10, uma de 20 e uma de 50.
Temos que saber como podemos formar os outros 120,00. Vamos dividir em casos:
– Se ele não possuir mais notas de 50, teremos que formar 120,00 com notas de 10 e 20:
São 7 opções: 12 notas de 10; 1 de 20 e 10 de 10; 2 de 20 e 8 de 10; 3 de 20 e 6 de 10; 4 de 20 e 4 de 10; 5 de 20 e 2 de 10; 6 de 20.
– Se ele possuir mais uma nota de 50, teremos que formar 70,00 com notas de 10 e 20:
São 4 opções: 7 notas de 10; 1 de 20 e 5 de 10; 2 de 20 e 3 de 10; 3 de 20 e 1 de 10.
– Se ele possuir mais duas notas de 50, teremos que formar 20,00 com notas de 10 e 20:
São 2 opções: 1 de 20 ou 2 de 10.
Verificamos que o número de casos possíveis é 7 + 4 + 2 = 13
Para contarmos o número de casos favoráveis, devemos considerar as opções onde ele tem pelo menos duas notas de 50, ou seja, 4 + 2 = 6.
Probabilidade = 6/13
Resposta: D
Questão 2 (BB – Cesgranrio). Uma moeda não tendenciosa é lançada até que sejam obtidos dois resultados consecutivos iguais. Qual a probabilidade de a moeda ser lançada exatamente três vezes?
(A) 1/8
(B) 1/4
(C) 1/3
(D) 1/2
(E) 3/4
Resolução:
Primeira jogada: qualquer resultado serve (probabilidade igual a 1)
Segunda jogada: só serve o resultado que não aconteceu da primeira vez (probabilidade igual a ½)
Terceira jogada: só serve o mesmo resultado que aconteceu na segunda jogada (probabilidade igual a ½)
Logo: 1 x ½ x ½ = ¼
Resposta: B
Questão 3 (BB – FCC). Para disputar a final de um torneio internacional de natação, classificaram-se 8 atletas: 3 norte-americanos, 1 australiano, 1 japonês, 1 francês e 2 brasileiros. Considerando que todos os atletas classificados são ótimos e têm iguais condições de receber uma medalha (de ouro, prata ou bronze), a probabilidade de que pelo menos um brasileiro esteja entre os três primeiros colocados é igual a:
(A) 5/14
(B) 3/7.
(C) 4/7.
(D) 9/14.
(E) 5/7
Resolução:
Dica: Quando aparecer na questão “pelo menos um”, devemos encontrar a probabilidade de não acontecer nenhum, ou seja, de não termos brasileiros no pódio, e depois diminuirmos de 1.
Probabilidades:
De nenhum brasileiro ganhar ouro = 6/8 = 3/4
De nenhum brasileiro ganhar prata = 5/7 (desconsideramos a medalha de ouro)
De nenhum brasileiro ganhar bronze = 4/6 = 2/3 (desconsideramos as medalhas de ouro ou prata)
Então:
P (não termos brasileiros no pódio) = 3/4 x 5/7 x 2/3 = 5/14
P (termos pelo menos um brasileiro no pódio) = 1 – 5/14 = 14/14 – 5/14 = 9/14
Resposta: D
Questão 4 (BB – Cesgranrio). Uma urna contém 5 bolas amarelas, 6 bolas azuis e 7 bolas verdes. Cinco bolas são aleatoriamente escolhidas desta urna, sem reposição. A probabilidade de selecionar, no mínimo, uma bola de cada cor é
Resolução:
Sejam os eventos:
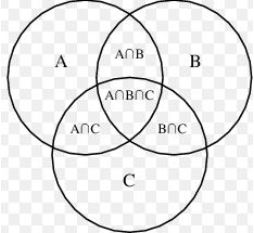
A = Selecionar amarelas
B = Selecionar azuis
C = Selecionar verdes
Queremos calcular a probabilidade de selecionarmos pelo menos uma bola de cada cor, ou seja, P(A∩B∩C).
Veja no diagrama ao lado que P(A∩B∩C) = P(A∪B∪C) – P(A∪B) – P(A∪C) – P(B∪C) + P(A) + P(B) + P(C)
Temos que:
Resposta: A
Questão 5 (TRT – CESPE). Em 2007, no estado do Espírito Santo, 313 dos 1.472 bacharéis em direito que se inscreveram no primeiro exame do ano da Ordem dos Advogados do Brasil (OAB) conseguiram aprovação.
Em 2008, 39 dos 44 bacharéis provenientes da Universidade Federal do Espírito Santo (UFES) que fizeram a primeira fase do exame da OAB foram aprovados.
Com referência às informações contidas nos textos acima, julgue os itens a e b que se seguem.
a) Se um dos bacharéis em direito do estado do Espírito Santo inscritos no primeiro exame da OAB, em 2007, fosse escolhido aleatoriamente, a probabilidade de ele não ter sido um dos aprovados no exame seria superior a 70% e inferior a 80%.
Inscritos: 1472
Reprovados: 1472 – 313 = 1159
1159/1472 = 0,787 = 78,7%
Resposta: CERTO
b) Considerando que, na primeira fase do exame da OAB de 2008, 87,21% dos bacharéis em direito da Universidade Federal de Pernambuco (UFPE) tenham sido aprovados, a probabilidade de se escolher ao acaso um dos aprovados entre os bacharéis da UFPE que fizeram esse exame será maior que a probabilidade de se escolher ao acaso um dos aprovados entre os bacharéis da UFES e que também fizeram o exame da OAB.
Probabilidade de se escolher um aprovado entre os alunos da UFPE: 87,21%
Probabilidade de se escolher um aprovado entre os alunos da UFES: 39/44 = 0,8864 = 88,64%
Resposta: ERRADO
Questão 6 (Caixa – CESPE). Leia o texto e as figuras abaixo e analise a veracidade das afirmações a e b.
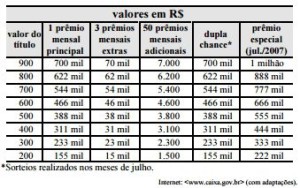
Conheça o título de pagamento único CAIXACAP DA SORTE, da CAIXA CAPITALIZAÇÃO, e dê mais chances à sua sorte. Você escolhe o valor que quer investir, de R$ 200,00 a R$ 900,00, múltiplos de R$ 100,00, paga uma única vez e concorre, todo mês, a 54 prêmios de até R$ 700 mil. E, ao final do prazo de capitalização, você recebe 100% do valor guardado, atualizado pela taxa referencial de juros (TR). Além dos sorteios mensais, tem o sorteio nos meses de julho durante a vigência do título, com premiação em dobro: serão 2 clientes contemplados com o prêmio de até R$ 700 mil. Além de tudo isso, em julho de 2007 ocorrerá o sorteio especial, quando você concorrerá durante 1 semana a 7 prêmios, um por dia, de até R$ 1 milhão, como mostra a tabela abaixo. Os sorteios serão realizados pela Loteria Federal do Brasil, sempre no último sábado de cada mês. Se você for sorteado, continua concorrendo, exceto ao sorteio especial, realizado em julho de 2007.
a) A probabilidade de um detentor de um título CAIXACAP DA SORTE ser sorteado durante a vigência do título é igual a 1/(36×54), independentemente do número total de detentores desses títulos.
Resolução
A probabilidade sempre depende da quantidade de concorrentes.
Resposta: ERRADO
b) Ao longo dos 36 meses de capitalização, o detentor de um único título CAIXACAP DA SORTE tem a possibilidade de ganhar no máximo R$ 1 milhão.
Resolução
O texto nos diz que o ganhador continua concorrendo, exceto pelo prêmio especial. Para provarmos que o enunciado está errado, basta imaginarmos um sortudo que ganhe 10 vezes o prêmio principal mensal.
Resposta: ERRADO
Questão 7 (PM PE – IAUPE). Dos 500 aprovados em um concurso, 205 falam inglês, 210, espanhol, e 65, ambos os idiomas. Escolhendo ao acaso um dos aprovados, qual a probabilidade de ele não falar nenhum desses idiomas?
a) 40%
b) 25%
c) 30%
d) 45%
e) 35%
Resolução
Total de alunos que falam algum idioma:
205 + 210 – 65 = 350
Veja que subtraímos os 65 alunos que falam os dois idiomas e estavam sendo contados duas vezes quando consideramos os 205 que falam inglês e os 210 que falam espanhol.
Total de estudantes que não falam nenhum idioma:
500 – 350 = 150
Probabilidade do estudante não falar nenhum idioma:
150/500 = 0,3 = 30%
Resposta: C
Questão 8 (Terezina – NUCEPE). Uma caixa contém 8 bolas verdes, 6 bolas amarelas, 4 bolas azuis e 2 bolas vermelhas. Qual a probabilidade, de alguém, sem olhar, tirar dessa caixa uma bola azul?
a) 10%.
b) 20%.
c) 40%.
d) 50%.
e) 100%.
Resolução
Observe que a caixa possui 4 bolas azuis e um total de 20 bolas.
A probabilidade de sair uma bola azul é:
4/20 = 0,2 = 20%
Resposta: B
Questão 9 (PC Pará – AOCP). Um grupo composto por cinco peritos, escolhidos entre sete possíveis peritos, deve ser formado para determinada investigação. Sabe-se que um dos possíveis peritos é do sexo masculino e os demais são do sexo feminino. A probabilidade de que esse grupo seja formado somente com peritos do sexo feminino é igual a
(A) 2/7 .
(B) 1/5 .
(C) 1/9 .
(D) 4/7 .
(E) 2/5 .
Resolução
O total de grupos de 5 pessoas formados a partir de 7 é o total de combinações de 7 elementos, tomados 5 a 5:
C(7,5) = 7×6/2×1 = 21
O total de grupos de 5 mulheres a partir de 6 disponíveis é o total de combinações de 6 elementos, tomados 5 a 5:
C(6,5) = 6
Calculando a probabilidade:
6/21 = 2/7
Resposta: A
Espero que todos tenham curtido nossos exercícios resolvidos sobre probabilidade.
Saber Matemática, o melhor site de matemática para concursos.




Um grupo de amigos organiza uma loteria cujos bilhetes são formados por 4 algarismos distintos. Qual é a probabilidade de uma pessoa, possuidora dos bilhetes 1387 e 7502, ser premiada, sendo que nenhum bilhete tem como algarismo inicial o zero?
2/4536 = 0,000440917
gostei muito,agora estou pronta para prova.
Que bom que gostou Jessiane,
Continue acessando e aprendendo sempre mais…
Ola Boa tarde.
Poderia me tirar uma dúvida?!
1) O quadro funcional de uma empresa é composta de 35 pessoas efetivas e 15 prestadoras de serviço. Do pessoal efetivo 20 são homens e do pessoal prestador de serviço 5 são mulheres. Escolhendo aleatoriamente uma pessoa dessa empresa, a probabilidade dessa pessoa ser homem ou prestador de serviço é:
* 20%
*70%
*90%
*60%
*80%
30/50 + 15/50 – 10/50 = 30/50 = 0,7 x 100 = 70%
**** 60%. Já que 30/50 = 0,6 . 0,6 x 100 = 60% (:
oi. Da onde você tirou esse -10/50 ?
Oi Aline,
Os 30/50 são o total de homens (20 efetivos e 10 prestadores de serviço)
Os 15/50 são o total de prestadores de serviço
Esses -10/50 representa o total de homens que também são prestadores de serviço porque em cima se você perceber eles são contados duas vezes(uma vez no total de homens e outra nos prestadores) aí subtraímos para que não sejam contados de novo.
olá, acho que o resultado está correto, mas é 35/50 e não 30/50
NÃO SERIA – MENOS 15/50 PARA DAR 70%
bom dia peso ajuda com a resolucao deste problema
1. Suponha que a UCM emprega 2000 membros do sexo masculino e 500 do sexo feminino. A lei da igualdade das oportunidades de emprego, sugere a criação de uma amostra aleatória estratificada de 200 elementos do sexo masculino e outros 200 do sexo feminino.
a) Qual é a oportunidade de um membro do sexo feminino ser escolhido para integrar a amostra?
b) Qual é a oportunidade de um membro do sexo masculino ser escolhido?
c) A cada elemento da amostra é colocada a questão: – ” Na sua opinião, os membros do sexo feminino desta universidade são, em geral, mais mal pagos do que os do sexo masculino, quando desempenham as mesmas funções e têm as mesmas qualificações?”
180 das 200 senhoras (90 por cento) responderam que ”sim”
60 dos 200 homens (30 por cento) responderam que ”sim”
Daqui se conclui que 240 elementos da amostra de 400 sujeitos (60 por cento) responderam que ”sim” e o coordenador deste estudo registou o seguinte: ”…. “aseado numa amostra, podemos concluir que 60 por cento dos membros de toda a Universidade pensam que as senhoras recebem vencimentos mais baixos do que os homens.”
Explique porque razão esta conclusão está errada. Qual deveria ser essa percentagem?
Peço neste exercício. Em uma escola 30% dos estudantes estão no curso de Humanidade e o resto em Ciências sociais. O 40% dos que cursam Humanidade São mulheres e os cursam ciência São 20% São homens. Elegendo um estudante ao acaso, a) Qual é a probabilidade de ser homem?
b) Qual é a probabilidade de ser mulher?
Por favor como seria a resolução dessa questão:
Cada uma das 13 letras do nome “SANTA CATARINA” é escrita em
um cartão e todos os cartões são colocados em uma urna.
Aleatoriamente, são então retirados, sucessivamente e sem
reposição, dois cartões.
A probabilidade de um dos cartões retirados conter a letra S e o
outro cartão retirado conter a letra C é de:
Acredito que seja 1/156 ou 0,641%
Quantidade de letras S=1
Quantidade de letras C=1
Como na questão ele pede a primeira com S E(multiplicação) a segunda com C, sem reposição dos cartões, temos:
P(AeB)=(1/13)x(1/12)=1/156
Obrigada Rafael.
Mas no gabarito a resposta era 1/78. Acredito que soma-se 1/156 (a primeira pode ser S ou C) + 1/156 (a segunda pode ser S ou C) = 2/156=1/78
Gisele,
Bom, na verdade a explicação é o seguinte: Como o exercício não está pedindo se os cartões estão em ordem de retiradas, na primeira vez que eu for retirar, posso tirar tanto o S como o C, fazendo com que eu tenha 2 possibilidades em 13, após retirado 1 cartão, sobrarão 12, se eu tirei o C na primeira tentativa, agora precisarei tirar o S e vice versa, então só me sobrará 1 possibilidade em 12, pois não houve reposição.
Multiplicando os eventos distintos:
2/13 * 1/12 = 2/156 ou 1/78
Por favor, como resolvo este problema: No patio do detran um inspetor encarregado de vistoriar 10 carros, sendo 5 carros de cor prat, 3 carros de cor preta e 2 carros de cor vermelha. Para iniciar inspecoes ele sorteou aleatoriamente, de uma unica vez, dois desses carros . A probabilidade de que pelo menos um dos dois carros sorteados seja de cor prata e igual a…
eu acho que é de 50% a chance de sair um carro da cor prata pois se tem 5 , ou seja corresponde a metade do valor total de carros !
POXA EU ACHO QUE É 90% POIS 30/50 É A QUANTIDADE DE HOMENS , 15/50 DE PRESTADORES DE SERVIÇO ,ENTÃO 30/50 : 0.6 , 15/50 : 0.3 E O RESTANTE SÃO DE MULHERES OU SEJA 0.1 ,0.6+0.3 :0.9 X 100 : 90 % !
Caríssimos,
Podem responder, por favor?
1.Um novo produto de consumo foi desenvolvido por pesquisadores com base no fato de que 50% de todos os consumidores são homens. Considere uma amostra de 400 compradores selecionada aleatoriamente.
Calcule a probabilidade de o número de homens dessa amostra ser maior do que 175.
2.Considere o salário semanal dos trabalhadores operários de uma indústria de construção civil distribuído normalmente em torno de uma média de $ 80,00, com desvio-padrão de $ 5,00
Calcule o valor do salário para selecionarmos 10% dos operários com maiores remunerações.
Grata!
Boa noite, conseguiu fazer o exercício 1?
Obrigado
Por favor , poderiam me responder?
Um casal pretende ter quatro filhos. Qual a prob. de serem dois meninos e duas meninas ?
Obrigada
P= n (e) / n (a) = 2/4 = 0,5 x 100 = 50%
. A caixa X tem 8 objetos, sendo que 3 são defeituosas. A caixa Y tem 5 objetos, sendo que 3 deles são defeituosos. Um
objeto é retirado aleatoriamente de cada caixa. Se um deles é defeituoso, e o outro não, então a probabilidade de o
defeituoso ter vindo da caixa X é igual a
A) 5/19
B) 7/19
D) 19/40
C) 9/19
E) 9/40
Por gentileza qual seria a resposta dessa questão?
Os dados meteorológicos de determinada localidade indicam que, nos últimos 100 anos, a temperatura máxima do primeiro dia de verão excedeu a 75 graus em 79 dos anos.
a) Estime a probabilidade de que tal ocorra o primeiro dia de verão deste ano.
b) Que hipótese levantou quanto à comparabilidade dos anos? É razoável essa hipótese?
Uma Turma de estatística é composta de 23 homens e 27 mulheres. Vamos sortear 3 alunos para participarem de uma comissão de formatura. Qual a probabilidade de que a comissão seja formada:
a) Somente por homens?
b) por 1 homem e 2 mulheres?
Boa noite!Gostaria que me auxilia-se na resolução das seguintes questões:
1-Numa população onde 40% dos indivíduos têm alguma descendência indígena, retira-se uma
amostra aleatória de 4 pessoas. Qual é a probabilidade de se encontrar:
(a) exatamente 2 pessoas com descendência indígena?
(b) mais de 2 pessoa(s) com descendência indígena?
2-Um grupo de 16 elementos apresenta a seguinte composição:
Categoria Homens Mulheres
Menores 8 2
Adultos 5 1
(a) Qual a probabilidade de ser homem?
(b) Qual a probabilidade de ser adulto?
(c) Qual a probabilidade de ser menor e mulher?
(d) Sabendo-se que o elemento escolhido ´e adulto, qual a probabilidade de ser homem?
(e) Dado que a escolhida ´e mulher, qual a probabilidade de ser menor
Em uma população, a probabilidade de um indivíduo está estressado é 1/25. Quando um individuo está estressado, a probabilidade dele se recuperar é 1/4, portanto qual a probabilidade de um individuo dessa população, escolhido aleatoriamente se recuperar? Qual a solução para esta questão?
Olá Nísia! Favor enviar a sua dúvida através do fórum do nosso site.
gente uma ajuda por favor com uma questão!? 9) Na lista de chamada de uma turma, os 30 alunos são numerados de 1 a 30. Em certo dia quando faltaram os alunos de números 11 e 26, o professor sorteou um aluno para resolver uma atividade na lousa. Qual é a probabilidade de o número do aluno que irá a lousa ser: A) menor que 9 B) múltiplo de 4 C) primo D) primo E) maior que 12 e menor que 25
a- 2/7
b- 1/4
c- 2/7
d- 2/7
e- 3/7
Abaixo tem-se os tempos de ruptura de quinze corpos de prova de concreto, em segundos.
2,34 3,02 3,12 3,14 3,79 4,21 4,50 4,77 5,12 5,13 5,55 6,10 6,46 6,29 0,38
Encontre os limites inferior e superior do gráfico Box-plot para esta amostra e baseado neles, verifique se há algum tempo que pode ser considerado não usual (fora do padrão).
O tempo de fabricação de uma lâmpada segue uma distribuição uniforme no intervalo [10,12], onde o valor é medido em dias. A empresa considera a produção como eficiente se foi produzida em menos de 10 dias e 12 horas. Determine a probabilidade da fábrica produzir eficientemente uma lâmpada.
Renata está grávida e realizará um exame que detecta o sexo do bebê. Se o exame detectar que é um menino, a probabilidade de ela pintar o quarto do bebê de azul é de 70%, ao passo que de branco é de 30%. Mas, se o exame detectar que é uma menina, a probabilidade de ela pintar o quarto do bebê de rosa é de 60% contra 40% de pintar de branco. Sabendo-se que a probabilidade de o exame detectar um menino é de 50%, a probabilidade da Renata pintar o quarto do bebê de branco é de
a) 70%
b) 50%
c) 35%
d) 30%
e) 20%
Alguém pode me ajudar com esse exercício? sei que a resposta é 35 %, mais quero saber como chegar lá passo a passo.
Três brasileiros , dois espanhóis e um alemão disputarão uma corrida.Determine a probabilidade de um brasileiro termina em primeiro lugar e o alemão terminar em segundo lugar.Alguém pode me ajudar nesse exercício?
Francisco, entendo que 3 brasileiros, 2 espanhóis e 1 alemão, perfazendo um total de 6 pessoas. Se um dos brasileiros termina em 1º , então é 3 em 6; agora só sobraram 5 para concorrerem o 2º lugar, então é 1 em 5. O “e” é multiplicação: 3/6 x 1/5 = 3/30 = 1/10 = 10%
Tais, Bom Dia. desculpe-me a demora, mas só hoje é que vi a sua solicitação. Entendo que a maior dificuldade desta questão é que as letras A),B),C),D) e E), não são alternativas de resposta, mas são itens a serem calculados. são 30 alunos (o de número 11 e o de número 16 faltaram) então o meu espaço amostral foi reduzido para 28. Qual a probabilidade de o numero do aluno sorteado ser:
A) menos que 9? (1,2,3,4,5,6,7,8) = 8/28 =2/7
B) múltiplo de 4? (4,8,12,16,20,24,28) = 7/28 = 1/4
C) e D) primo (2,3,5,7,11,13,17,19,23) o de número 11 não pode ser sorteado porque faltou à aula. Logo só são 8/28 = 2/7
E) de 13 a 24, tudo depois do 11 e antes do 26, portanto os dois faltosos não influenciam o numerador.
logo o cálculo será 12/28 =3/7.
Espero ter lhe ajudado para os próximos concursos.
Ola, tenho uma questão que gostaria de ver se alguem tem como resolver
Consideremos três apostadores chamados A, B e C. Eles lançam
sucessivamente uma mesma moeda com probabilidade de dar cara igual
a 1/2, na ordem a seguir:
O apostador A lança primeiro, logo segue B e finalmente C. O jogo consiste
em lançar a moeda até obter a primeira cara. Ganha o jogo o apostador
que conseguir obter primeiro uma cara. Assuma que os lançamentos são
independentes. Indique qual é a probabilidade do apostador B ganhar o
jogo.
mais uma questão que preciso de ajuda, desenvolvi e encontro resultado diferente do gabarito.Num grupo de 10 pessoas, há 4 homens e 6 mulheres. Dentre os homens
3 são canhotos e dentre as mulheres 2 são canhotas. Selecionadas duas
pessoas aleatoriamente e sem reposição do grupo, qual a probabilidade
de que a amostra contenha pelo menos uma pessoa destra ou pelo menos
uma mulher?
encontro 7/15 e gabarito diz 14/15
Gostei muito da aula
Obrigado Nurce,
Volte sempre!
As explicacões são claras deu para perceber, mas não tanto para fazer-me perceber o exercício q tenho a resolver, me podiam ajudar?
Uma empresa paga um bônus para quatro funcionários A, B, C e D.
A recebe quatro vezes tanto quanto B
B recebe 50% do valor pago a c
C e D obtêm o mesmo valor.
Se o total for 180.000, quanto receberá cada um?
Olá, podem me ajudar com essa questão?
Se há 0,70 de probabilidade de uma pessoa entrevistada ser a favor do candidato A em uma eleição, qual a probabilidade de:
a) As duas primeiras pessoas entrevistadas serem contra?
b) As duas primeiras pessoas entrevistadas serem contra, mas a terceira ser a favor?
A. 0.3×0.3=0.9. B.0.3×0.3×0.7=0.063
Uma pesquisa realizada com 280 pessoas fez o levantamento da
frequência anual de visitas ao dentista. Os resultados aparecem na tabela
abaixo.
Número de
visitas ao
dentista por ano
Número
de
pessoas
0
63
1
105
2
39
3
47
4
16
5 ou mais
10
Total
280
Responda:
A) Qual é o número mediano de visitas?
B) Quantas pessoas dessa amostra que visitam o dentista uma única vez
por ano deveriam passar a visitá-lo duas vezes por ano a fim de que a
mediana passasse a ser 1,5 visita?
Em um casino a aposta no jogo é de 400 usd e se ganhar o casino paga 12000 usd. A probabilidade de acertar é 1/38, quanto o casino espera ganhar por cada aposta?
As probabilidades de que haja 1, 2, 3, 4 ou 5 pessoas em cada carro que vai a Guriri num sábado são, respectivamente: 0,05; 0,20; 0,40; 0,25 e 0,10. Qual o numero médio de pessoas por carro?
Escolha uma:
a. Aproximadamente 3.
b. Aproximadamente 4
c. Aproximadamente 2
d. Aproximadamente 1
e. Aproximadamente 5
Astrogildo deseja vender seu carro e está estudando a possibilidade de fazer propaganda. Estima-se que é de 0,4 a probabilidade de que ele o venda pelo preço estipulado de R$ 1500,00 sem propaganda e de 0,9 a probabilidade de que ele o venda com propaganda. Suponha que se não o vender por R$1500,00 ele o venderá a uma agência por R$1100.00. Determine o valor da propaganda, de tal modo que sua expectativa seja a mesma, faça ele propaganda ou não.
Escolha uma:
a. R$250,00
b. R$200,00
c. R$190,00
d. R$220,00
e. R$195,00
Usa-se um aparelho de radar para medir a velocidade dos carros numa rodovia principal de uma cidade na hora do “pico”. As velocidades dos carros seguem o modelo normal de probabilidade com média 50km/h e desvio padrão 5Km/h. Determinar de que a velocidade de um carro esteja ente 55 e 60.
Escolha uma:
a. 0,8116
b. 0,4772
c. 0,3413
d. 0,1359
alguém poderia me ajudar?
Em um processo produtivo de semicondutores a probabilidade de um componente ser defeituoso é de 0,3. Pretende-se realizar uma retirada de 20 peças, defina as seguintes probabilidades:
a) Obter exatamente 9 peças boas?
b) Obter 9 peças defeituosas?
c) Obter 3 defeitos ou menos?
d) Obter mais de 3 peças boas?
Por favor. Preciso disso para hoje.
19) Em uma experiência aleatória foi lançado duas vezes um dado.
Considerando que o dado é equilibrado, determine:
a) A probabilidade de conseguir no primeiro lançamento o número 5 e no segundo o número 4;
b) A probabilidade de obter em pelo menos um dos lançamentos o número 5;
c) A probabilidade de obter o mesmo número em ambos os lançamentos;
d) A probabilidade de obter a soma dos lançamentos igual a 5;
e) A probabilidade de obter a soma dos lançamentos igual ou menor que 3.
Alguém poderia explicar esse dado na questão 1? Não entendi.
“Para contarmos o número de casos favoráveis, devemos considerar as opções onde ele tem pelo menos duas notas de 50, ou seja, 4 + 2 = 6.”
50 lançamentos são suficientes para obter uma precisão de uma casa decimal no valor da probabillidade estimada p(d) de ganho? justifique sua resposta
cinco amigos, duas raparigas e tres rapazes decidiram ir ao cinema. compram bilhetes e dirigem se para a sala de sessoes, onde sentam aleatoriamente em cinco lugares seguidos, previamente reservados.
a) Qual e a probabilidade das raparigas sentarem juntas?
b) qual e a probabilidade das raparigas ficarem juntas e os rapazes tambem?
Ola Boa tarde Dr. Gostaria de ter algumas aulas de probabilidade, principalmente aquelas relacionadas com a formula de Bayes.
ME AJUDA AI .
Antes do inicio de um jogo de futebol , ” Bahia X Vitoria ” o juiz sorteia , entre o capitães dos dois times , o lado em que cada um dos times irá jogar para isso , lança uma moeda para o ar e verifica ao cair se deu cara ou coroa . O capitão do time do Bahia escolheu cara . A probabilidade de ser esse capitão a escolher o lado do campo será de :
a) 15%
b) 20%
c) 35%
d) 40%
e) 50%
COMO SÃO TOTAL DUAS POSSIBILIDADES UMA CARA DAI FICA 1/2 = 50%
PERGUNTA 4
Pedro é um aluno de engenharia em uma determinada universidade em Salvador e tem 70% de chance de responder corretamente cada questão de uma prova de cálculo A. Sabendo-se que essa prova é composta de 10 questões objetivas, cada uma valendo 1 ponto, assinale a alternativa que indica a probabilidade de Pedro tirar, exatamente, nota 7 e ser aprovado na disciplina.
26,68%.
24,68%.
20,68%.
22,68%.
28,68%.
O número médio de ligações recebidas por segundo por uma central de telemarketing é igual a 3 ligações/segundo. Assumindo a distribuição de Poisson, que , assinale a alternativa que indica a probabilidade de que a central receba duas ou menos ligações por segundo em um determinado dia.
0,56.
0,24.
0,42.
0,38.
0,67.