Estudando matemática para concursos? Confira aqui tudo sobre o princípio da casa dos pombos, também conhecido como princípio das gavetas.
Não deixe de ver também os nossos conteúdos sobre os outros tópicos da análise combinatória.
Bom estudo!
Vamos imaginar que temos que colocar 5 pombos em 4 casas. O que podemos afirmar com certeza é que em alguma casa haverá mais de um pombo. Sempre que a quantidade de pombos for maior que a quantidade de casas, alguma casa abrigará mais de um pombo. Foi estudando esses tipos de problemas que desenvolveu-se o Princípio da Casa dos Pombos.
Da mesma forma, se eu tenho um armário com 3 gavetas e possuo 4 meias que são guardadas nessas gavetas, também posso afirmar que uma das gavetas conterá mais de uma meia. Por isso o estudo deste tipo de problema também é chamado de Princípio das Gavetas.
De fato, trata-se da mesma coisa. Como é mais usual, a partir de agora vamos utilizar somente a expressão Princípio da Casa dos Pombos.
Para entendermos melhor o princípio, vamos voltar ao exemplo inicial das 4 casas para 5 pombos.
Vamos tentar colocar um pombo em casa casa:
- O primeiro pombo será colocado na casa 1;
- O segundo na casa 2;
- O terceiro na casa 3;
- O quarto na casa 4;
- E o quinto? Obrigatoriamente terá que escolher uma casa que já está ocupada.
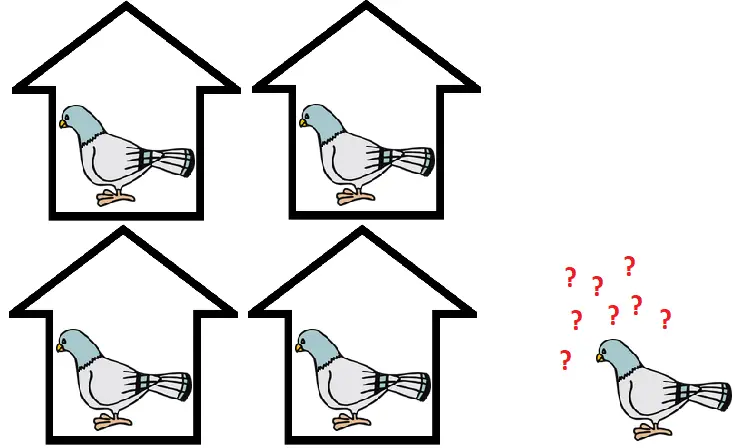
Podemos resumir o Princípio da Casa dos Pombos da seguinte forma:
Se tivermos n + 1 pombos para serem colocados em n casas, então pelo menos uma casa deverá conter dois ou mais pombos.
Matematicamente falando, quando o número de elementos de um conjunto finito A é maior do que o número de elementos de um outro conjunto B, então uma função f: A → B não pode ser injetiva.
Dicas para resolver exercícios envolvendo o Princípio da Casa dos Pombos:
- Identificar quais são as “casas” e quais são os “pombos”;
- Organizar os pombos nas casas;
- Verificar a relação entre pombos e casas.
Exemplo 1: Quantos alunos devem ter em uma sala de aula, de modo que tenhamos certeza de que pelo menos dois deles fazem aniversário no mesmo mês?
Podemos considerar:
Casas: meses
Pombos: alunos
Relação: aluno com o respectivo mês de aniversário
Pelo Princípio das Gavetas, se tentarmos “encaixar” um aluno em cada mês, o 13º aluno fará aniversário no mesmo mês de outro aluno. Assim, podemos concluir que se existirem 13 alunos, pelo menos dois deles farão aniversário no mesmo mês.
Exemplo 2: Uma urna contém 4 tipos de bolas (vermelhas, pretas, rosas e brancas). Quantas bolas devemos retirar, de modo que possamos garantir que tenhamos duas bolas da mesma cor?
Quando retiramos as 4 primeiras bolas da caixa, a pior hipótese possível é que cada uma seja da mesma cor.
Assim, é necessário retirar uma quinta bola para garantirmos que haverá repetição de cor.
Exemplo 3: Em um laranjal existem 50 pés de laranja. Sabemos que cada uma delas não produz mais do que 60 laranjas por temporada. Será que existem pés de laranja que produzem a mesma quantidade de frutos?
Casas: quantidade de laranjas
Pombos: Pés de laranja
Vamos considerar a pior situação possível, onde os 50 primeiros pés de laranja produziram 1, 2, 3, 4, …, 50 frutos, respectivamente. Neste caso, obrigatoriamente, os outros 10 pés de laranja deveram repetir a quantidade de frutos. De onde podemos afirmar que existem, pelo menos, dois pés com a mesma quantidade de laranjas.
O que achou do Princípio da Casa dos Pombos?
Deixe o seu comentário.
No exemplo número 3, a quantidade de pés de laranja e quantidade de frutos produzidos não deveriam ser o inverso: 60 pés de laranja e 50 laranjas produzidas no máximo por pé??
Oi Gláucia!
Caso a quantidade de plantas fosse maior, a resposta seria Não.