Confira aqui vários exercícios resolvidos sobre o cálculo do volume de um cubo, todos retirados dos últimos concursos públicos.
Não deixe de ver também nossos exercícios resolvidos sobre os outros tópicos da geometria espacial.
Bom estudo!
Questão 1 (PM ES – Exatus 2013). Determinado cubo possui volume de 729 cm³. Cada face desse cubo possui área de:
a) 3 cm2.
b) 9 cm2.
c) 27 cm2.
d) 54 cm2.
e) 81 cm2.
Resolução
O objetivo da questão é descobrir a área de cada face do cubo. Para tanto, precisamos descobrir a medida de cada aresta (a).
A única informação que temos é que o volume do cubo é de 729 cm³.
Utilizando a fórmula do volume:
V = a³
729 = a³
a = 9 cm
Calculando a área de cada face, sabendo que as faces têm o formato de um quadrado e que cada aresta do cubo mede 9 cm:
A = a²
A = 9²
A = 81 cm²
Resposta: E
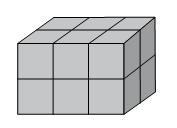
Questão 2 (SAP SP – VUNESP 2011). Os produtos de uma empresa são embalados em caixas cúbicas, com 20 cm de aresta. Para transporte, essas embalagens são agrupadas, formando um bloco retangular, conforme mostrado na figura. Sabe-se que 60 desses blocos preenchem totalmente o compartimento de carga do veículo utilizado para o seu transporte. Pode-se concluir, então, que o volume máximo, em metros cúbicos, transportado por esse veículo é
a) 4,96.
b) 5,76.
c) 7,25.
d) 8,76.
e) 9,60.
Resolução
O primeiro passo é calcular o volume de cada caixa. Como as respostas estão apresentadas em metros cúbicos, vamos considerar que cada aresta mede 0,2 m (20 cm).
Vc = a³
Vc = 0,2³
Vc = 0,008 m³
Pela figura, percebe-se que um bloco retangular contém 12 caixas. Vamos calcular o volume de cada bloco:
Vb = 12 . 0,008 = 0,096 m³
Para finalizar, cabem 60 blocos no caminhão. Calculando o volume total:
Vt = 60 . 0,096 = 5,76 m³
Resposta: B
Questão 3 (PM ES – Exatus 2013). Um estoquista, ao conferir a quantidade de determinado produto embalado em caixas cúbicas de arestas medindo 40 cm, verificou que o estoque do produto estava empilhado de acordo com a figura que segue:
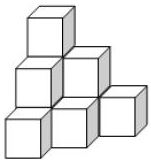
Ao realizar corretamente os cálculos do volume dessa pilha de caixas, o resultado obtido foi:
a) 0,64 m³
b) 1,6 m³
c) 6,4 m³
d) 16 m³
e) 64 m³
Resolução:
Pela figura, é possível observar que existem 10 caixas empilhadas.
Vamos calcular o volume de cada caixa, sabendo que cada aresta mede 0,4 m (40 cm):
V = a³
V = 0,4³
V = 0, 0,064 m³
Como existem 10 caixas:
Vt = 10 . 0,064 = 0,64 m³
Resposta: A
Questão 4 (SES DF – IADES 2014). Sabe–se que o volume de um cubo de aresta α é dado por α³ . Considerando que a aresta de um cubo seja multiplicada por 2, em quantas vezes seu volume aumentará?
a) Duas.
b) Três.
c) Quatro.
d) Seis.
e) Oito.
Resolução
Como foi informado, o volume de um cubo de aresta α é igual a α³. Vamos calcular o volume de um cubo de aresta 2α:
V = (2α)³
V = 2³.α³
V = 8.α³
Daí, quando multiplicamos a aresta do cubo por 2, o volume para a ser 8 vezes maior.
Resposta: E
Questão 5 (SEDUC RJ – COPERJ 2013). A figura abaixo representa uma caixa cúbica onde a distância do ponto A até o ponto B mede 3√5 decímetros:
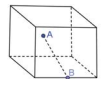
Os pontos A e B são, respectivamente, o centro de uma face e o ponto médio de uma aresta da face oposta. O volume dessa caixa, em dm³ , é igual a:
a) 125
b) 216
c) 343
d) 512
e) 729
Resolução
Precisamos calcular o volume do cubo representado na figura. Nosso primeiro objetivo é calcular a medida da aresta desse cubo, que representaremos inicialmente por x.
Vamos analisar o triângulo retângulo formado pela semi reta AB e pelas semi retas que dividem as faces ao meio. Veja a figura:
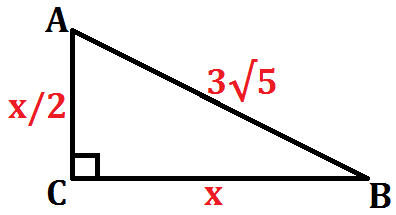
Pelo Teorema de Pitágoras temos:
(3√5)² = x² + (x/2)²
45 = x² + x²/4
45 = 5x²/4
5x² = 4.45
5x² = 180
x² = 180/5
x² = 36
x = 6 dm
Calculando o volume do cubo:
V = x³
V = 6³
V = 216 dm³
Resposta: B
Questão 6 (SEJUS ES – 2013). A quantidade de certo líquido, correspondente a 3/4 de um litro, será colocado em um recipiente de modo que ele fique completamente cheio. Para isso foram selecionados 3 recipientes com formas geométricas e medidas internas descritas a seguir:
I. Um paralelepípedo reto retângulo de dimensões: comprimento 15 cm, largura 2,5 cm e altura 20 cm.
II. Um cilindro reto de raio da base 5 cm e altura 10 cm. (use π = 3)
III. Um cubo de aresta igual a 5 cm.
Dos 3 recipientes oferecidos, atende ao que foi proposto
(A) I e II, apenas.
(B) I, II e III.
(C) I, apenas.
(D) I e III, apenas.
(E) II e III, apenas.
Resolução
Para resolvermos a questão devemos ter o conhecimento prévio que 1 litro pode ser colocado em um recipiente de 1000 cm³.
Nosso objetivo será descobrir quais dos 3 recipientes possuem volume equivalente a 750 cm³ (3/4 de 1000 cm³).
Calculando:
I) Volume do paralelepípedo
V = comprimento x largura x altura = 15 x 2,5 x 20 = 750 cm³
II) Volume do cilindro
V = área da base x altura = π.5².10 = 3.25.10 = 750cm³
III) Volume do cubo
V = lado³ = 5³ = 125cm³
Apenas os recipientes I e II.
Resposta: A
Questão 7 (Bombeiros ES – 2011). Em uma unidade do Corpo de Bombeiros, os três reservatórios utilizados para armazenamento de água têm, respectivamente, os formatos cúbico, cilíndrico e cônico. O cubo tem arestas iguais a 1 m, o cilindro e o cone têm alturas iguais a 1 m, os raios das bases do cilindro e do cone são iguais a 0,5 m e o cone é circular reto. Considerando 3,14 o valor aproximado de π e desprezando as espessuras dos reservatórios, julgue a seguinte afirmação:
“A capacidade do reservatório cilíndrico é 78,5% da capacidade do reservatório cúbico.”
Resolução
Calculando a capacidade de cada um dos reservatórios:
Volume do cubo
V = 1³
V = 1 m³
Volume do cilindro
V = π x r² x altura
V = 3,14 x 0,5² x 1
V = 3,14 x 0,25
V = 0,785 m³
Resposta: A afirmação é verdadeira.
Espero que gostem dos nossos exercícios resolvidos sobre o volume de um cubo.
Saber Matemática, o melhor site de matemática para concursos.