Procurando exercícios resolvidos sobre o conjunto dos Números Reais?
Confira aqui uma seleção de questões resolvidas, todas retiradas dos mais diversos concursos públicos realizados pelo país.
Bom estudo e boa sorte!
Questão 1 (CRA SC – IESES). Leia as frases abaixo sobre a teoria dos conjuntos:
I. {0, 1, 2, 3, 5} pertencem ao conjunto dos Números Naturais.
II. A raiz quadrada de 2 é um Número Irracional.
III. Os Números Reais são formados pela intersecção dos Números Racionais e os Irracionais.
IV. Todo número inteiro não positivo pertence ao conjunto dos Números Naturais.
A sequência correta é:
a) Apenas as assertivas I e II estão corretas.
b) Apenas as assertivas II e III estão corretas.
c) Apenas as assertivas I, II e III estão corretas.
d) Apenas as assertivas I, III e IV estão corretas.
Resolução:
Vamos analisar caso a caso:
I) Afirmativa correta. Sabemos que os números naturais são os números inteiros e não negativos.
II) Afirmativa correta. Como √2 não tem um valor exato, trata-se de um número irracional.
III) Afirmativa incorreta. A interseção dos racionais com os irracionais é um conjunto vazio. O correto seria que os Reais são a união entre esses dois conjuntos.
IV) Afirmativa incorreta. Os números inteiros não positivos são formados pelo zero e pelos inteiros negativos, que logicamente não são naturais.
Resposta: A
Questão 2 (Espcex 2006). Se x é racional e y é irracional, então:
a) x . y é racional.
b) y . y é irracional.
c) x + y é racional.
d) x – y + √2 é irracional.
e) x + 2y é irracional.
Resolução:
Vamos analisar caso a caso, lembrando que se existir um caso onde a afirmação não vale, então toda a afirmação é falsa.
a) Falsa. Veja que 1.√2 = √2, que é irracional.
b) Falsa. Veja que √2.√2 = 2, que é racional.
c) Falsa. Veja que 0 + √2 = √2, que é irracional.
d) Falsa. Veja que 0 – √2 + √2 = 0, que é racional.
e) A questão é verdadeira pois a soma de um número racional com um número irracional é sempre um número irracional. Além do mais, o dobro de um número irracional é sempre um número irracional.
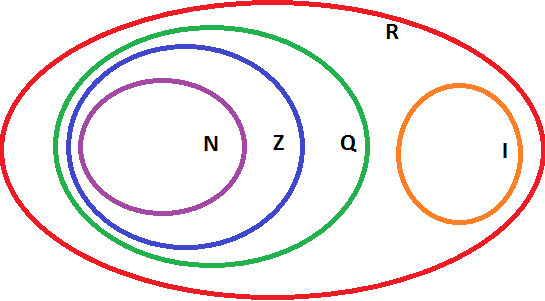
Questão 3 (Pref. Teresina – NUCEPE). Considerando os conjuntos: ℝ (números reais), ℝ\ℚ (números irracionais), ℚ (números racionais), ℤ (números inteiros) e ℕ (números naturais). Qual das seguintes afirmações não é verdadeira?
a) ℝ⋃(ℝ\ℤ)=ℝ
b) (ℕ⋃ℤ)⋃(ℚ⋃ℝ\ℚ)=ℝ
c) ℕ⋂ℤ=ℕ
d) ℚ⋃ℤ⋃ℕ=ℝ
e) (ℕ⋃ℚ)⋂ℝ=ℚ
Resolução
O conjunto dos números reais (ℝ) é a união do conjunto dos números racionais com o conjunto dos números irracionais.
Observe que a igualdade ℚ⋃ℤ⋃ℕ=ℝ não é verdadeira pois não temos o conjunto dos números irracionais.
Resposta: D
Gostou dos nossos exercícios resolvidos sobre o conjunto dos números reais?
Deixe o seu comentário.