Confira nesta página uma seleção especial de exercícios resolvidos sobre cálculo de área do círculo, todas retiradas das últimas provas de concursos.
O assunto é muito atual e cai em praticamente todas as provas que cobram geometria plana.
Bom estudo!
Questão 1 (PM ES – Exatus 2013 – adaptada). Laura cultiva flores em um canteiro com formato de semicírculo, cujo diâmetro mede 16 m. A área ocupada por esse canteiro é igual a:
a) 256π m²
b) 128π m²
c) 64π m²
d) 32π m²
e) 16π m²
Resolução:
Como o diâmetro do círculo mede 16 m, o raio mede 8 m.
Calculando a área do círculo:
A = π.r²
A = π.8²
A = 64π m²
A área do semicírculo será a metade da área do círculo: 32π m²
Resposta: D
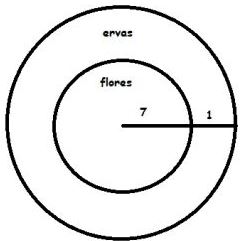
Questão 2 (CFO PM ES – Exatus 2013). Adriana planta flores num canteiro circular de raio 8 m. Ao redor desse canteiro, ela pretende plantar ervas medicinais formando uma coroa circular, de maneira que a parte destinada às flores sofrerá uma redução de 2 m em seu diâmetro. A área ocupada pelas ervas medicinais neste canteiro será igual a:
a) 13π
b) 14π
c) 15π
d) 16π
e) 8π
Resolução
Adriana plantava em um circulo cujo raio mede 8 metros. Como ela vai plantar ervas medicinais em volta, reduzindo em 2 metros o diâmetro, o raio passará a medir 7 metros.
A área ocupada pelas ervas medicinais será a diferença entre as áreas dos circulo cujos raios medem 8 e 7 metros.
A = π.8² – π.7²
A = 64π – 49π
A = 15π
Resposta: C
Questão 3 (CEPERJ – SEPLAG 2013). A razão entre a área e o perímetro de uma circunferência de raio R vale:
a) R/π
b) π/2
c) πR/2
d) 2R
e) R/2
Resolução
Para resolvermos a questão, basta relembrarmos as fórmulas utilizadas para o cálculo da área do do perímetro de uma circunferência:
A = π.R²
P = 2π.R
Calculando a razão:
![]()
Resposta: E
Questão 4. (SESC PA – Coned 2016). Qual o valor da área do círculo inscrito num quadrado, se a área do círculo circunscrito a esse quadrado mede 32π cm² ?
a) 10 π cm²
b) 8 π cm²
c) 16 π cm²
d) 12 π cm²
e) 9 π cm²
Resolução
O primeiro passo para resolvermos a questão é calcular o raio do círculo circunscrito, do qual já sabemos a medida da sua área. Vamos utilizar a fórmula que calcula a área em função do raio:
A = π.r²
32π = π.r²
r² = 32
r = 4√2
Podemos observar na figura abaixo que o raio que achamos é a metade da diagonal do quadrado, onde podemos formar o triângulo retângulo ABC, cujo lado BC mede exatamente o raio do círculo inscrito no quadrado.
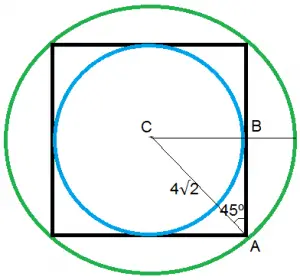
Temos:
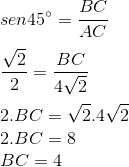
Agora que já sabemos o raio do circulo inscrito, podemos calcular sua área:
A = π.r²
A = π.4²
A = 16π cm²
Resposta: C