Confira diversos exercícios resolvidos sobre sistemas lineares, matéria que está na moda em várias bancas de concursos público pelo país.
Lembrando que os exercícios a seguir foram todos retirados de provas de concursos e apresentam uma resolução detalhada para você aprender de vez essa matéria.
Bom estudo!
Questão 1 (PM SP 2014 – Vunesp). Em um lote de xícaras de porcelana, a razão entre o número de xícaras com defeitos e o número de xícaras perfeitas, nesta ordem, é 2/3. Se o número total de xícaras do lote é 320, então, a diferença entre o número de xícaras perfeitas e o número de xícaras com defeitos, nesta ordem, é:
(A) 56.
(B) 78.
(C) 93.
(D) 85.
(E) 64.
Resolução:
Vamos denominar:
x = número de xícaras com defeitos
y = número de xícaras perfeitas
Sabendo disto, temos as seguintes equações:
x/y = 2/3, ou seja, x = 2y/3
x + y = 320
Temos um sistema de equações de primeiro grau. Substituindo a primeira na segunda equação:
2y/3 + y = 320 (multiplicando ambos os lados por 3)
2y + 3y = 320.3
5y = 960
y = 960/5 = 192
Calculando x:
x = 2y/3 = 2.192/3 = 128
Daí,
y – x = 192 – 128 = 64
Resposta: E
Questão 2 (PM SP 2014 – Vunesp). Com determinada quantidade de dinheiro é possível comprar 5 revistas em quadrinhos, todas de mesmo valor e, ainda, sobram R$ 2,50. Porém, se com a mesma quantia de dinheiro forem compradas 7 revistinhas de palavras cruzadas, cada uma delas de mesmo valor, sobrarão R$ 0,50. Sabendo que uma revistinha de palavra cruzada custa R$ 1,00 a menos que uma revistinha em quadrinhos, então, o preço de uma revistinha de palavras cruzadas é:
(A) R$ 3,50.
(B) R$ 4,90.
(C) R$ 4,60.
(D) R$ 3,80.
(E) R$ 4,20.
Resolução:
Seja x o valor de cada revista em quadrinhos e y o valor de cada palavra cruzada.
Pela afirmação: “é possível comprar 5 revistas em quadrinhos, todas de mesmo valor e, ainda, sobram R$ 2,50. Porém, se com a mesma quantia de dinheiro forem compradas 7 revistinhas de palavras cruzadas, cada uma delas de mesmo valor, sobrarão R$ 0,50.”, temos:
5x + 2,50 = 7y + 0,50
Pela afirmação: “uma revistinha de palavra cruzada custa R$ 1,00 a menos que uma revistinha em quadrinhos”, temos
y = x – 1,00
Note que temos duas equações com duas variáveis, ou seja, um sistema de primeiro grau. Substituindo a segunda na primeira equação:
5x + 2,50 = 7(x – 1,00) + 0,50
5x + 2,5 = 7x – 7 + 0,5
7x – 6,5 = 5x + 2,5
7x – 5x = 2,5 + 6,5
2x = 9
x = 9/2 = 4,50
Calculando y:
y = x – 1,00 = 4,50 – 1,00 = 3,50
Resposta: A
Questão 3 (PM SP 2014 – Vunesp). Uma pessoa foi a uma livraria e escolheu três livros: um romance, um de aventuras e um de ficção, porém, por motivos financeiros, decidiu que levaria apenas dois deles. Se comprar o romance e o livro de aventura, pagará R$ 53,00; se comprar o romance e o livro de ficção, pagará R$ 58,00 e, se comprar o livro de ficção e o livro de aventura, pagará R$ 55,00. O valor dos três livros juntos é:
(A) R$ 83,00.
(B) R$ 80,00.
(C) R$ 72,00.
(D) R$ 75,00.
(E) R$ 70,00.
Resolução:
Seja R o valor do livro de romance, A o valor do de aventura e F o valor do de ficção.
Da afirmação: “Se comprar o romance e o livro de aventura, pagará R$ 53,00;”, temos:
R + A = 53
Da afirmação: “se comprar o romance e o livro de ficção, pagará R$ 58,00”, temos:
R + F = 58
Da afirmação: “se comprar o livro de ficção e o livro de aventura, pagará R$ 55,00”, temos:
F + A = 55
Vamos somar as três equações:
R + A + R + F + F + A = 53 + 58 + 55
2R + 2A + 2F = 166
2(R + A + F) = 166
R + A + F = 166/2
R + A + F = 83
Resposta: A
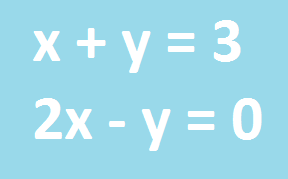
eu quero aprende mas sobre sistema linear