Caros estudantes, nesta página veremos alguns exercícios resolvidos de derivadas. Tentaremos apresentar da maneira mais simples possível, pois sabemos que o conteúdo não é apresentado no ensino médio.
O assunto não costuma cair em muitos concursos, mas pode ser utilizado como uma importante ferramenta para resolver questões com mais agilidade.
1) Calcule a derivada das funções abaixo:
a) f(x) = x²
Resposta:
f'(x) = 2x
b) f(x) = 20
Resposta:
f'(x) = 0
c) f(x) = 5x³ + 2x
Resposta:
f'(x) = 3.5x² + 2 = 15x² + 2
d) f(x) = x³ + 1000
Resposta:
f'(x) = 3x²
e) f(x) = x³ + x² + x + 1
Resposta:
f'(x) = 3x² + 2x + 1
2) Calcule a derivada das funções abaixo, utilizando a Regra da Cadeia:
a) f(x) = (x² + 1)³
Resposta:
Veja que temos f(x) = h(g(x)), onde:
h(x) = x³
g(x) = x² + 1
Temos então:
b) f(x) = sen(x²)
Resposta:
Veja que temos f(x) = h(g(x)), onde:
h(x) = sen(x)
g(x) = x²
Temos então:
f'(x) = cos(x²).2x = 2x.cos(x²)
Resposta:
Veja que temos f(x) = h(g(x)), onde:
Temos então:
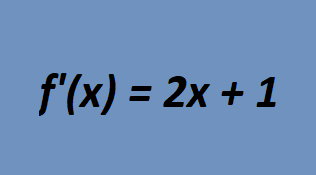
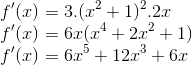
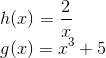
Esclarecedoras suas aulas
Professor, gostei muito das explicações . Espero continuar visitando esta pagina.Agradeço sinceramente pela vossa ajuda.
Obrigado Edvaldo. Volte sempre!
muuito obrigadooo
Professor derivei e não obtive sua resposta, referente a este item a) f(x) = (x² + 1)³, minha derivada deu 6(x²+1)²
Thalia,
você deve observar que a derivada de x²+1 é 2x.
a derivada de f(x) = x^2 e igual a 2x
f(x)=x^2
R: 2*x^2-1
2x^-1
2x
Professor, gostaria do desenvolvimento passo a passo da seguinte questão:
A derivada de ([2senx^2/3cosx^2]2) é:
Desde já agradeço!
Professor Jordon, você poderia me dizer qual é a derivada do ln(xy²)?
Desde já agradeço!
Olá Breno,
Temos duas variáveis.
Caso queira a derivada em relação a x, deve considerar y constante.
Caso queira a derivada em relação a y, deve considerar x constante.
Procure derivadas implicitas.
Resumindo se voce considerar a derivada em relação a X, quando derivar o Y coloque dy/dx ao lado, depois é só isolar o dy/dx em um lado da igualdade.
Preciso que me forneçam o conteúdo relaccionado ao Trabalho Mecanico aplicando derivadas
Caso eu não estiver conectado agradeceria se me passasses pelo meu facebook.com/belchiorlo
Espero deferimento senhor professor
boa tarde Achei muito legal o site..
queria ver se pode me ajudar como resolvo f(x)= x²+2 em x= 3
obrigada
Olá Fernanda!
f(x)= x²+2
f'(x)= 2x
f'(3)= 2.3 = 6
H(x)=(x³-3)² derivada ,sabendo que temos que usar a regra da cadeia
como faço para calcular a derivada de f(x) = x²+2 em x=3
Olá Josilda!
f(x)= x²+2
f'(x)= 2x
f'(3)= 2.3 = 6
Muito Clara a explicaçao, Obrigado professor. Eu estou nesse momente enfrentando alguns problemas com as derivadas mais com a explicaçaoo acima estou entendendo um pouco como funciona isso.
Professor, bom dia. Como faço para encontrar a derivada da função u= t+5 / t – 7
Olá Romero!
u = t + 5/t – 7
u = t + 5.t-¹ – 7
u’ = 1 – t-²
u’ = 1 – 1/t²
Espero ter ajudado.
Ola bom dia, estou tendo duvida no momento em que voce colocou o t-7 para cima, voce colocou somente o t^-1, achei que teria que fazer isso com -7 tambem, o meu ficou assim:
u = (t+5).(t-7)^-1
u = 1.-1(t-7)^-2
u = 1.-1/t^2
Gostaria dessa ajuda, desde ja agradeco a atencao.
Olá Tobias!
Neste caso os parênteses fazem toda a diferença.
Eu resolvi considerando que não existem parênteses.
Professor como faço para derivar essa função y=b/a √a²-x²?
Olá Diogo!
Você pode resolver utilizando a regra da cadeia.
Por favor me ajude a
encontra reta tangente a curva abaixo no ponto x=3
y=2.3x² – 3x -4
Olá Jordan!
Vou considerar 2,3x²…
O primeiro passo é descobrir a coordenada y deste ponto:
y = 2,3.3² – 3.3 – 4 = …
O segundo passo é calcular a inclinação da reta tangente, onde utilizaremos os conceitos de derivada:
y’ = 4,6x – 3
No ponto x = 3:
y’ = 4,6.3 – 3 = …
Sabendo a inclinação de uma reta e um ponto pertencente a ela, é possível determiná-la através da equação reduzida da reta:
y = mx + n, onde m é a inclinação.
Espero ter ajudado!
(2x-3)^4*(x^2+x+1)^5 como que faço isso
pode me ajudar a resolver 3 questões de derivada da função?
f(x)=(3x²+ 4 sobre X⁷ +1) elevado a 10
g(x)=(X⁴ – x)elevado a -3 . (5-x²)-¹
f(x) = 3√x sobre x³ +1
e) f(x) = x³ + x² + x + 1
Resposta: f'(x) = 3x² + 2x + 1 Esta incorreta
resposta certa: 3x² + 2x
Desculpe Camila, mas você está equivocada.
Esta correta porque a derivada de x é 1 então fica 3x° +2x+1
Esta certo a resposta é 3x^2+2x+1
Derivada de x é 1.
Uma dica é sempre lembra de diminuir o grau de todos os elementos.
PROFESSOR TENHO MUITA DUVIDA EM DERIVADA .EX; G(X)=SENX²
Olá Luciene!
Você deve utilizar a regra da cadeia.
No seu caso o parênteses faz toda a diferença. É sen(x²) ou (senx)² ?
[-ln(x√x+1)]
[cos(x+cos(x+cos(x)))]
Olá eu não sou bem um perito ou um profissional em derivação, mas utilizando a regra da cadeia que aprendi a derivada de [cos(x+cos(x+cos(x)))] ficaria da seguinte forma:
-sen(x+cos(x+cos(x+cos(x)) . 1 – sen(x+cos(x)) . 1 – sen(x)
[x^5+4x^3/3-5/x^3]
[cos(x)sen(x)]
-senx.cosx
Se aí no meio de seno de x e cosseno de x tem uma multiplicação, utilizando os conhecimentos que obtive isso ficaria :
-sen(x) . sen(x) + cos(x) . cos(x)
não sei se devia fazer mas aprendesse errando também peço a vossa ajuda, eu pensei da seguinte sera que posso fazer isso:
-1( -sen(x) . sen(x)) + cos^2 x
[2-x/2+x] derivada
y = (2 – x / 2 + x)
y´= [(2 – x)´ . ( 2 + x) – (2 + x)´ . (2 – x)] / (2 – x)^2
y´= [ -1 . (2 + x) -1. (2 – x)] / (2 – x) ^ 2
y´= ( -2 – x -2 + x) / (2 – x) ^ 2
y´= ( -4 ) / (2 – x) ^ 2
f(x)=2x elevado a 5 tecnicas de derivação
f(x) = 2X ^5
f(x)´=5 . 2x ^5 – 1
f(x)´= 10x^4
como resolvo sen(5/3x) o x esta enfrente da fraçao
José,
acho que você quer saber a derivada de sen(x.5/3).
Regra da cadeia:
cos(x.5/3).(5/3)
professor como aplicar a regra da cadeia para determinar a derivada da função F(x) = cos (x3 + 2)
Olá Suyane,
F(x) = cos(x³+2)
F'(x) = -sen(x³+2).3x²
5x^2-3x+7 como q calcula a derivada primeira dessa equação?
Olá Jucineia!
f(x) = 5x² – 3x + 7
f'(x) = 10x – 3
Olá, tenho dois problemas:
2/3 × (5x-3)^-1 × 5x+3
Eu sei que para começar a calcular esta primeira derivada é preciso por o (5x-3)^-1 em:
1/5x-3, porque é mesma coisa
E a outra derivada é:
2/2x-1 – 1/x
Isso para calcular apenas a 1a derivada
Agradecia que me ajudasse
Boa iniciativa Professor Jordon continua assim
CARO PROFESSOR,
BOA TARDE
PODE POR FAVOR DIZER-ME A DERIVAÇÃO DA FUNÇÃO ABAIXO:
f(x)= x-2Vx+x²
Olá Vladimir!
A letra V está na função em qual contexto?
raiz quadrada
f (x) x-1÷ x+ 3
Encontre f'(x)
Calcula, aplicando a definição de derivada de uma funcao num ponto:
F (x)=2/x’ no ponto x=3
f(x)=x².ex
f(x) = x².e^x
f(x)’ = (x²) ‘ . e^x + (e^x) ‘ . x²
f(x)’ = 2x.e^x + e^x.x²
espero ter ajudado.
moçambique
Boa tarde,estou com esse desafio.O Sr pode me ajudar:
Y=2.lnx+^2 e y’=2/x+2x
Pode dar a solução detalhada?
Boa noite! na alternativa b: Sen(x^2) não posso fazer pela propriedade da multiplicação de derivadas?
fiz e não bateu
Olá Eva!
Não temos um produto de funções.
Eva. resoluçao desse exercicio seria:
sen(x²)
primeiro deves saber que é uma funçao composta.
deriva o argumento primeiro , neste caso o argumento é x², e depois vc sabe que derivada de sen(x) é cos(x)
logo sera: (x²) ‘ cos(x²) = 2x cos(x²). percebeu
aqui escrevo de moçambique
nao entendi a 2 segunda linha da 2 (a)
como faço essa questão:
Z= Y(2) senX / X
Integrando a função Receita Marginal podemos determinar a função Receita Total, ou
seja, conhecendo a forma de variar de uma função, podemos selecionar, de uma infinidade de
funções, uma família de funções com aquele comportamento, ou variação.
Sendo () = −60 + 3000, determine a função Receita Total
(0), considere o
(0) = 0 :
vanessa.
z = y² senx /x
nb. ai tens produto de funçoes, cujo outra funçao é uma divisao (quociente)
aplica regra de produto, depois do lado de quociente aplica regra do quociente.
z’ = (y²) ‘ . senx/x + (senx/x) ‘ . y²
z’ = 2y . senx/x + [ ( senx) ‘ . x – (x ) ‘ . senx /x²]
z’ = 2y .senx/x + cosx . x – cosx/x²
z’ = 2y.senx/x+cosx(x – 1/x²)
percebeu?
moçambique
Qual a derivada de raiz de 3x²+7x vezes 4/x^4?
qual a derivada de F(x)= e (elevado raiz de x^4-5x²+9x)+20
Dada a função f(x)=2×2−1 , calcule:
f ‘ (a) (a derivada de f em x=a), através da definição da derivada.
Sugestão: Você pode usar a igualdade abaixo
f'(a)=lim f(a+h)−f(a) h→0 h
Professor! Por gentileza, como faço para derivar y = x^5/3 + x^3/2. Muito obrigado!
Pode usar a derivada da potência (x^n)´ =nx^(n-1)
[x^(5/3) + x^(3/2)]`= (5/3) x^(5/3 -1) + 1,5x^(1,5-1) = (5/3) x^(2/3) + 1,5x^0,5.