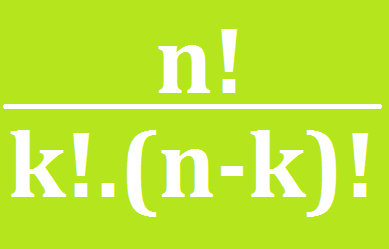Dando continuidade ao estudo da Análise Combinatória, vamos aprender a definição e a utilização da fórmula da combinação simples.
O assunto exige muita atenção do estudante e o ideal é que já tenha conhecimento acerca do cálculo do fatorial de um número natural.
Bom estudo!
O que é uma combinação simples?
Combinação simples é um agrupamento dos elementos distintos de um conjunto finito, onde a ordem é irrelevante.
Exemplo 1:
Em uma sala de aula existem 5 alunos que jogam vôlei (Antônio, Bernardo, Carlos, Davi e Elias).
A escola está promovendo um torneio interclasse de vôlei de areia, onde participam apenas dois jogadores.
Vamos listar as duplas que podem ser formadas escolhendo entre os 5 alunos citados:
- Antônio e Bernardo
- Antônio e Carlos
- Antônio e Davi
- Antônio e Elias
- Bernardo e Carlos
- Bernardo e Davi
- Bernardo e Elias
- Carlos e Davi
- Carlos e Elias
- Davi e Elias
Nota-se que podem ser formadas 10 duplas distintas a partir de um conjunto de 5 alunos.
Mas o mais importante a ser observado é que a dupla Antônio e Bernardo é igual a dupla Bernardo e Antônio, ou seja, a ordem é irrelevante.
Definição formal
Dado um conjunto A com uma quantidade n de elementos distintos, chamamos de combinação simples dos n elementos de A, tomados k a k, a qualquer subconjunto de A formado por k elementos.
Analisando o exemplo das duplas de vôlei, temos n = 5 e k = 2.
Fórmula
O exemplo utilizado para introduzir o conteúdo foi escolhido por ser possível listar rapidamente todas as possibilidades, porém existem casos onde listar todas as combinações poderia ser inviável.
Aprenderemos a utilizar a fórmula para calcular o número de combinações simples. Veja:
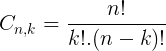
Onde:
Cn,k = quantidade de combinações simples
n = quantidade de elementos do conjunto
k = quantidade de elementos por arranjo
n ≥ k
Exemplo 2:
Uma pizzaria trabalha no formato “monte sua pizza”, onde o cliente pode escolher 9 entre 15 coberturas diferentes, de acordo com o seu gosto. Quantas pizzas diferentes é possível montar neste formato?
Veja que temos que escolher 9 entre 15 sabores, sendo que pouco importa a ordem das coberturas, ou seja, temos que calcular a quantidade de combinações de 15 elementos, tomados 9 a 9.
Utilizando a fórmula de combinações:
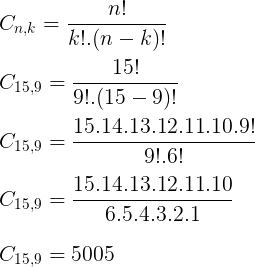
Exemplo 3:
Uma classe com 40 alunos deseja escolher 4 deles para formar uma comissão de formatura. Quantas comissões diferentes podem ser formadas?
Veja que pouco importa quem será escolhido primeiro, ou seja, temos que calcular a quantidade de combinações de 40 alunos, tomados 4 a 4.
Utilizando a fórmula de combinações:
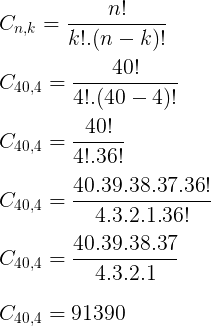
Gostou da nossa publicação sobre combinação simples?
Deixe o seu comentário.