Vamos aprender a calcular o volume do paralelepípedo oblíquo? Nesta página você verá a fórmula utilizada e alguns exemplos.
Não deixe de ler também nossos outros conteúdos sobre geometria espacial.
Bom estudo!
Um paralelepípedo oblíquo é aquele onde as arestas laterais não formam um ângulo reto (90º) com a base. Neste caso, para calcularmos o volume, devemos primeiramente descobrir a altura. Veja:
Seja o paralelepípedo abaixo, onde:
- os lados a, b e c;
- as arestas laterais formam um ângulo x com a base
- a base é um retângulo.
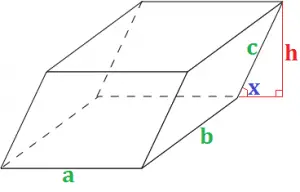
Podemos descobrir a medida da altura h em função do lado c e do ângulo x.
Analisando o triângulo retângulo formado na figura, temos:
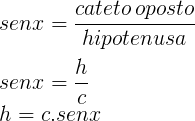
Agora que calculamos a medida da altura, basta efetuarmos o cálculo do volume do prisma, onde:
Volume = (área da base) . (altura)
Volume = a . b . c . senx
Obs: Caso a base seja um paralelogramo e não um retângulo, a fórmula para o cálculo do volume do paralelogramo oblíquo será:
Volume = Ab . c . senx
Onde:
Ab = área do paralelogramo
Exemplo 1. Calcular o volume do paralelogramo oblíquo abaixo, sabendo que a base é um retângulo:
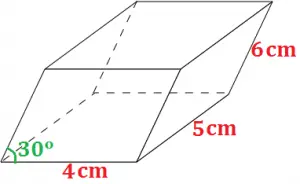
Utilizando a fórmula:
Volume = a . b . c . senx
Volume = 4 . 5 . 6 . sen30º
Volume = 120 . 1/2
Volume = 60 cm³
Exemplo 2. Calcular o volume do paralelepípedo oblíquo abaixo, sabendo que a base é um quadrado.
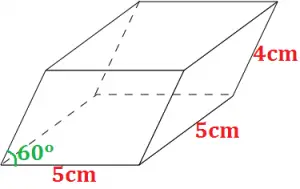
Utilizando a fórmula:
Volume = a . b . c . senx
Volume = 5 . 5 . 4 . sen60º
Volume = 100 . √3/2
Volume = 50√3 cm³
