Olá amigos de Moçambique! Devido a nossa grande audiência neste lindo país, e após vários pedidos, apresentamos a resolução do Exame de Admissão UP 2020.

Boa sorte a todos!

Questão 1. Qual é o valor da expressão

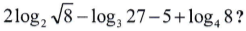
a) 2/7

b) -7/2

c) -2/7

d) 7/2

Resolução

Calcularemos separadamente o valor de cada logaritmo, considerando:

• log₂√8 = x

• log₃27 = y

• log₄8 = z

• Analisando o primeiro logaritmo, temos:

2^x = √8 = 8^1/2 = (2³)^1/2 = 2^3/2

Conclusão: x = 3/2

• Analisando o segundo logaritmo, temos:

3^y = 27 = 3³

Conclusão: y = 3

• Analisando o terceiro logaritmo, temos:

2^2z = 4^z = 8 = 2³

Conclusão: 2z = 3 e z = 3/2

Finalizando:

2.log₂√8 – log₃27 – 5 + log₄8

2.(3/2) – 3 – 5 + 3/2

3 – 3 – 5 + 3/2

-5 + 3/2

-7/2

Resposta: B

Questão 2. Qual é o valor da expressão

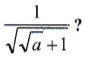
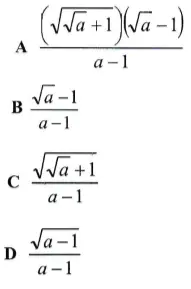
Resolução

Devemos simplificar uma expressão em formato de fração, cujo denominador é um radical.

O primeiro passo será multiplicar numerador e denominador pelo radical √(√a + 1).

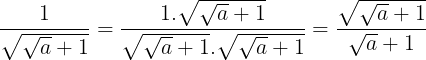
O próximo passo será multiplicar numerador e denominador pelo conjugado do denominador (√a – 1).

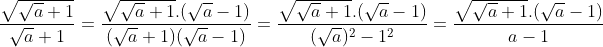
Resposta: A

Questão 3. Das três sentenças abaixo:

I. sen30° = cos60°

II. √3 + √2 = √5

III. {1, 2}∈[1, 2]

a) somente a II é verdadeira

b) somente a III é falsa

c) somente a III é verdadeira

d) somente a I é falsa

Analisando cada uma das sentenças:

I. Verdadeira. Observe na tabela de seno e cosseno que sen30° = cos60° = 1/2.

II. Falsa. Os valores aproximados dos radicais em questão são: √2 ≅ 1,41, √3 ≅ 1,73 e √5 ≅ 2,23.

III. Verdadeira. Os números 1 e 2 pertencem ao intervalo fechado [1, 2].

Resposta: Somente a II é falsa

Questão 4. A razão entre a idade de Pedro e a de seu pai é igual a 2/9. Se a soma das duas idades é igual a 55 anos, então Pedro tem

a) 12 anos

b) 13 anos

c) 10 anos

d) 15 anos

Resolução

Considere:

x = idade de Pedro

y = idade do pai de Pedro

Como a razão é igual a 2/9, temos:

x/y = 2/9 ⇒ 2y = 9x

Como a soma das idades é igual a 55 anos, temos:

x + y = 55 ⇒ y = 55 – x

Substituindo o valor de y na primeira equação:

2y = 9x

2(55 – x) = 9x

110 – 2x = 9x

110 = 9x + 2x

11x = 110

x = 110/11

x = 10 anos

Resposta: C

Questão 5. O número abaixo equivale a:

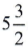
a) 15/2

b) 13/2

c) 11/2

d) 8/2

Resolução

Observe que temos o produto de um número inteiro por uma fração.

Neste caso, devemos multiplicar o número inteiro pelo numerador:

5.3/2 = 15/2

Resposta: A

Questão 6. Qual é a negação de p∧q?

a) ~p∧q

b) ~p∧~q

c) p∨~q

d) ~p∨~q

Resolução

O símbolo ∧ representa que as proposições simples p e q estão ligadas pelo conectivo lógico denominado conjunção (e).

Quando precisamos negar uma proposição composta ligada por este conectivo, basta negar as proposições simples e trocar o conectivo ∧ pelo ∨ (disjunção).

~(p∧q) = ~p∨~q

Resposta: D

Questão 7. Para construir a pipa representada na figura ao lado pelo quadrilátero ABCD, foram utilizadas duas varetas, linha e papel.

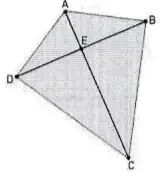
As varetas estão representadas pelos segmentos AC e BD. A linha utilizada liga as extremidades A, B, C e D das varetas, e o papel reveste a área total da pipa.

Os segmentos AC e BD são perpendiculares em E, e os ângulos ABC e ADC são retos. Se os segmentos AE e EC medem, respectivamente, 18 cm e 32 cm, determine o comprimento total da linha, representada por AB + BC + CD + DA.

a) 80 cm

b) 100 cm

c) 120 cm

d) 140 cm

Resolução

Considerando as informações do enunciado, temos a seguinte figura:

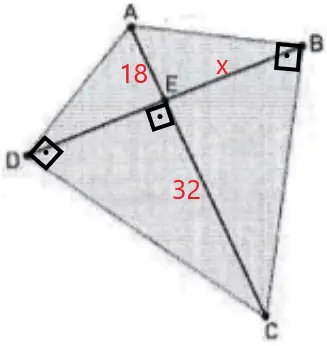
Observe os triângulos retângulos AEB e BEC. Podemos concluir que são triângulos semelhantes, pois:

• ambos possuem ângulos medindo 90°;
• os ângulos EBA e ECB são congruentes, pois ambos são complementares do ângulo EBC;
• por consequência, os ângulos EAB e EBC também são congruentes.

Considerando a semelhança de triângulos, e que x = EB, temos:

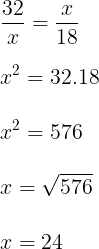
Podemos calcular os lados AB e BC através do Teorema de Pitágoras:

• No triângulo AEB:

AB² = 18² + 24²

AB² = 324 + 576

AB² = 900

AB = √900

AB = 30

• No triângulo BEC:

BC² = 24² + 32²

BC² = 576 + 1024

BC² = 1600

BC = √1600

BC = 40

Considerando as semelhanças de triângulo, temos que AB = DA e BC = CD.

Conclusão:

AB + BC + CD + DA = 30 + 40 + 40 + 30 = 140 cm

Resposta: D

Questão 8. Em R, qual é a solução da inequação

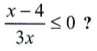
a) ]-∞; 4]

b) ]-∞; 0[ ∪ [4; +∞[

c) ]0; 4]

d) [4; +∞[

Resolução

Observe que a inequação apresenta uma divisão de duas funções:

f(x) = x – 4

g(x) = 3x

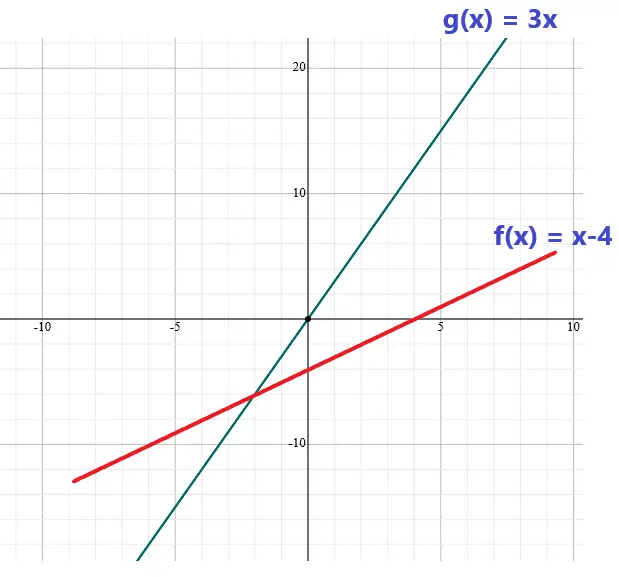
f(x) > 0 quando x > 0

g(x) > 0 quando x > 4

Teremos f(x)/g(x) ≤ 0 quando as funções possuírem sinais contrários, ou seja, x deve estar entre 0 e 4.

Para finalizar, devemos analisar os extremos:

0 não pode ser solução da inequação pois teríamos uma divisão por zero, que não está definida.

4 é solução da inequação, pois teríamos f(x)/g(x) = 0 ≤ 0.

Solução: ]0; 4]

Resposta: C

Questão 9. Sabe-se que o resto da divisão de um polinômio P(x) por binômio do tipo (x – a) é P(a). Qual é o resto da divisão de P(x) = 5x³ – 5x² + 5 por (x + 1)?

A) -1

B) 5

C) 1

D) -5

Resolução

Observe que o binômio (x + 1) possui a = -1.

Calculando o valor de P(a):

P(x) = 5x³ – 5x² + 5

P(-1) = 5(-1)³ – 5(-1)² + 5

P(-1) = 5.(-1) – 5.1 + 5

P(-1) = -5 – 5 + 5

P(-1) = -5

Resposta: D

Questão 10. Na tabela abaixo, estão indicados os preços do rodízio de pizzas de um restaurante.

Considere um cliente que foi a esse restaurante todos os dias de uma mesma semana, pagando um rodízio em cada dia.

Determine o valor médio que esse cliente pagou, em reais, pelo rodízio nessa semana.

a) 300

b) 400

c) 100

d) 200

Resolução

O cliente pagou 277,50 durante 4 dias, e 330,00 durante 3 dias.

Neste caso, devemos calcular a média aritmética ponderada:

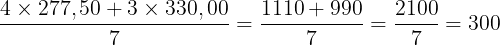
Resposta: A

Questão 11. A figura abaixo exibe o gráfico de uma função y = f(x). Então o gráfico de y = 2.f(x – 1) é dado por

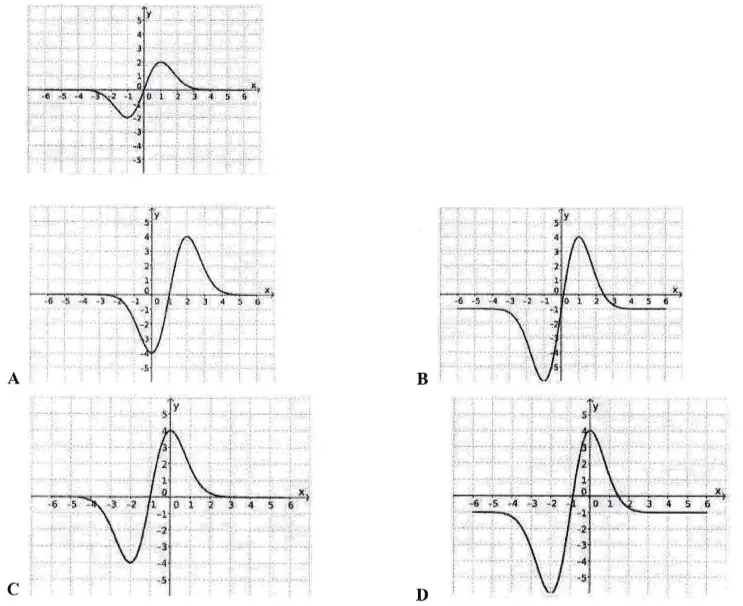
Resolução

Observe que a função f sofreu duas transformações:

1. y = f(x – 1)
2. y = 2.f(x – 1)

A primeira transformação faz com que o gráfico da função seja deslocado uma unidade para a direita.

A segunda transformação faz com que o gráfico da função seja “esticado” na vertical na proporção 2:1.

Como exemplo, observe as mesmas transformações no gráfico de y = x²:

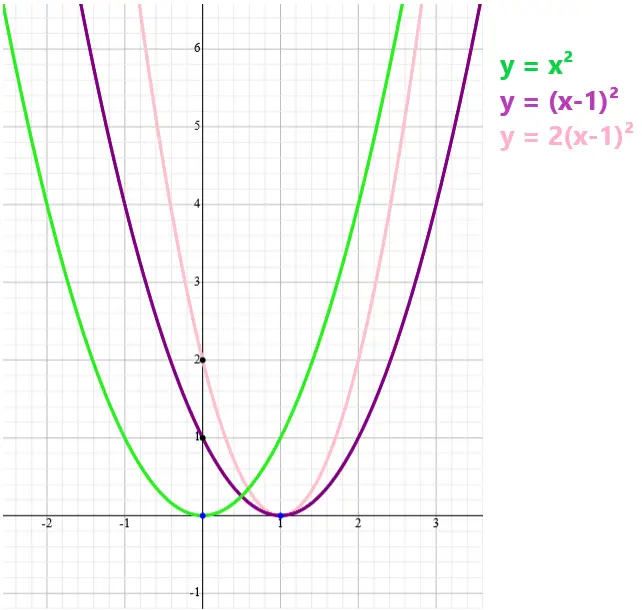
Deslocando o gráfico da questão uma casa para a direita, e “esticando” na proporção 2:1, teremos o gráfico da letra A.

Resposta: A

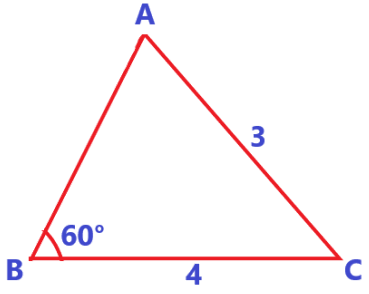
Questão 12. Considere um triângulo ABC, temos AC = 3m, BC = 4m e B = 60°. Qual é o valor do sen(A)?

a) 2√3/3

b) 3√3/2

c) √3/3

d) Não faz sentido porque tal triângulo não existe

Resolução

Considerando as características do triângulo ABC descritas no enunciado, deveríamos ter um triângulo com as seguintes características (figura fora de escala):

Traçando a altura AD, de comprimento h, o lado BC será dividido em duas partes, de medidas “a” e “4-a”.

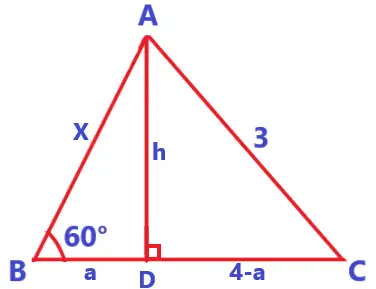
Aplicando o Teorema de Pitágoras nos dois triângulos retângulos:

• No triângulo ABD:

x² = a² + h²

• No triângulo ADC:

3² = h² + (4 – a)²

9 = h² + 16 – 8a + a²

Temos duas equações. Faremos a subtração da primeira pela segunda:

x² – 9 = a² + h² – (h² + 16 – 8a + a²)

x² – 9 = a² + h² – h² – 16 + 8a – a²

x² – 9 = – 16 + 8a

x² = 9 – 16 + 8a

x² = 8a – 7

Sabendo que cos60° = 1/2, em ABD temos:

cos60° = a/x

1/2 = a/x

a = x/2

Sabendo que x = 2a, substituiremos o valor de “a” na equação x² = 8a – 7:

x² = 8a – 7

x² = 8(x/2) – 7

x² = 4x – 7

x² – 4x + 7 = 0

Temos uma equação do segundo grau. Calculando o valor de delta:

Δ = b² – 4ac

Δ = (-4)² – 4.1.7

Δ = 16 – 28

Δ = – 12

Como Δ < 0, podemos concluir que não existe x (real) que satisfaz a equação, ou seja, o triângulo não existe.

Resposta: D

Questão 13. Para comprar os produtos A e B em uma loja, um cliente dispõe da quantia x, em meticais. O preço do produto A corresponde a 2/3 de x, e o do produto B corresponde à fração restante. No momento de efetuar o pagamento, uma promoção reduziu em 10% o preço de A. Sabendo que, com o desconto, foram gastos 350,00 Mts na compra dos produtos A e B. Qual é o valor, em meticais, que o cliente deixou de gastar.

A) 25,00mt

B) 35,00mt

C) 45,00mt

D) 15,00mt

O cliente possui x meticais para comprar os produtos A e B, sendo que o preço de cada produto é igual a:

A = x.2/3

B = x/3

No momento do pagamento, o preço de A foi reduzido em 10%, ou seja, passou a ser:

A . 90% = x . 2/3 . 9/10

A . 90% = x . 3/5

Sabendo que ele gastou 350 meticais, temos:

A.90% + B = 350

x.3/5 + x/3 = 350

(9x + 5x)/15 = 350

14x/15 = 350

x = 350.15/14

x = 375

Nota-se que o cliente tinha 375, porém pagou apenas 350 meticais, deixando de gastar 25.

Resposta: A

Questão 14. Considere o gráfico da função. Para quais valores de x a função é crescente?

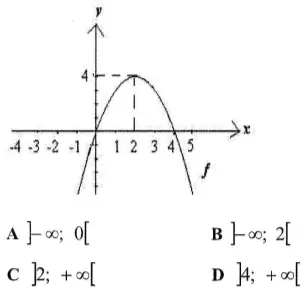
Resolução

A função é crescente para x < 2 e decrescente para x > 2.

O intervalo onde x é menor que 2 pode ser representado por ]-∞, 2[.

Observe que temos um intervalo aberto em 2 pois neste ponto a função não é crescente nem decrescente.

Resposta: B

Questão 15. Sejam A = [0, 8], B = [2, +∞[ e o Universo U = R. Qual é o resultado da operação

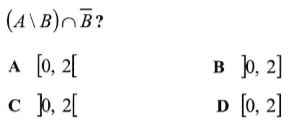
Resolução

Calculando A\B, os elementos que pertencem a A e não pertencem a B são representados pelo intervalo [0, 2[.

O complementar de B representa os números que não pertencem a B e estão no Universo R, ou seja, ]-∞, 2[.

Para finalizar, devemos calcular a interseção [0, 2[ ∩ ]-∞, 2[.

Veja que os números que pertencem aos dois intervalos podem ser representados pelo intervalo [0, 2[.

Resposta: A

Questão 16. A solução da equação abaixo na variável real x é um número

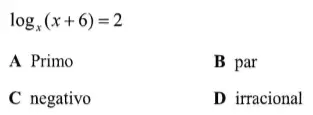
Resolução

Pela definição de logaritmos, temos:

x² = x + 6

x² – x – 6 = 0

Podemos resolver a equação do segundo grau pelo método da soma e produto:

S = -b/a = -(-1)/1 = 1

P = c/a = -6/1 = -6

Os dois números cuja soma é igual a 1 e o produto é igual a -6 são os números -2 e 3.

Como x representa a base do logaritmo, que deve ser maior que zero e diferente de 1, descartamos a solução -2.

Finalizando, 3 é um número primo.

Resposta: A

Questão 17. O triplo do valor de x que verificam a igualdade abaixo é

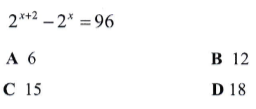
Resolução

A equação exponencial pode ser resolvida colocando em evidência a potência 2^x, após utilizarmos a propriedade da multiplicação de potências de mesma base:

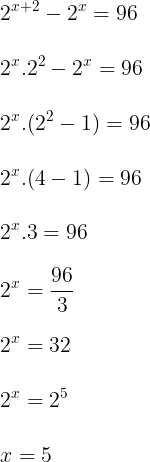
Calculando o triplo de x:

3x = 3.5 = 15

Resposta: C

Questão 18. Qual das seguintes expressões representam designação?

a) 3x – 4 > 2

b) 5x – 2 = 9

c) -3 + 15 = 18

d) 7 – 3.4

Resolução

Uma proposição lógica é uma afirmação que pode ser classificada como verdadeira ou falsa, enquanto uma designação é exatamente o contrário, pois não pode ser classificada desta forma.

Observe que podemos avaliar as alternativas A, B e C como verdadeiras ou falsas, porém não é possível afirmar isso na opção D.

Resposta: D

Questão 19. Qual é a proposição verdadeira?

Resolução

Analisaremos cada uma das alternativas:

A) A proposição diz que todos os números naturais satisfazem a equação. Isso não é verdade. Um contraexemplo simples é x = 1.

B) A proposição diz que existe um único número natural que satisfaz a igualdade. Isso não é verdade, pois o conjunto solução da equação possui dois números naturais: S = {0, 5}.

C) A proposição diz que todos os números inteiros satisfazem a equação. Já vimos que isso não vale para os naturais, e por consequência, também não vale para os inteiros.

D) A proposição diz que existe um número natural que satisfaz a equação. Basta utilizarmos x = 5.

x² – 5x = 5² – 5.5 = 25 – 25 = 0

Resposta: D

Questão 20. Qual é o domínio de definição da expressão abaixo?

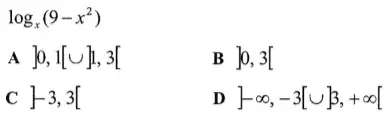
Resolução

A condição de existência do logaritmo log_BA, onde B é a base e A é o logaritmando, é:

• A > 0
• B > 0
• B ≠ 0

Analisando a base B, devemos ter x > 0 e x ≠ 1.

Analisando o logaritmando, devemos ter 9 – x² > 0. O estudo dessa inequação é feito através da função quadrática f(x) = 9 – x².

Essa função possui gráfico em formato de parábola com cavidade para baixo, considerando que a < 0. Também é fácil verificar que as raízes são -3 e 3.

Com essas informações, é possível desenhar o gráfico de f:

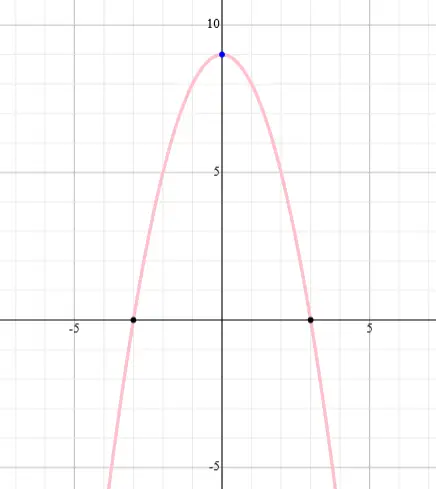
Veja que f(x) > 0 quando x∈]-3, 3[.

Finalizando, devemos ter x > 0, x ≠ 1 e x∈]-3, 3[, ou seja, x∈]0, 1[∪]1, 3[.

Resposta: A

Questão 21. Considerando a matriz abaixo, qual é o valor de k?

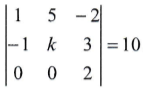
a) 1

b) 2

c) -1

d) 0

Resolução

Temos uma matriz 3×3, cujo determinante pode ser calculado da seguinte forma:

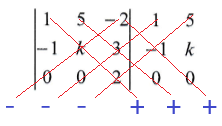
1.k.2 + 5.3.0 + (-2).(-1).0 – 0.k.(-2) – 0.3.1 – 2.(-1).5 = 10

2k + 0 + 0 – 0 – 0 + 10 = 10

2k = 10 – 10

2k = 0

k = 0

Resposta: D

Questão 22. Qual é o conjunto solução da inequação modular |1 – 2x|>5?

a) x ∈ ]-2, 3[

b) x ∈ ]3, +∞[

c) x ∈ ]-∞, -2[ ∪ ]3, +∞[

d) x ∈ ]-∞, -2[

Passando o 5 para o lado esquerdo da inequação modular, temos:

|1 – 2x| – 5 > 0

Analisando o módulo, 1 – 2x = 0 quando x = 1/2.

• Se x < 1/2:

1 – 2x – 5 > 0

-4 – 2x > 0

2x < -4

x < -4/2

x < -2

• Se x ≥ 1/2:

– (1 – 2x) – 5 > 0

-1 + 2x – 5 > 0

-6 + 2x > 0

2x > 6

x > 6/2

x > 3

Conclusão: x deve ser menor que -2 ou maior que 3, ou seja, x ∈ ]-∞, -2[ ∪ ]3, +∞[.

Resposta: C

Questão 23. Quantas palavras diferentes de três letras (com ou sem sentido na língua portuguesa) pode-se escrever com as letras da palavra CAMPUS?

a) 60

b) 20

c) 5

d) 24

Resolução

Devemos formar palavras de três letras, com ou sem sentido, podendo escolher entre 6 letras (C, A, M, P, U e S).

Temos 6 opções para escolhermos a primeira letra.

Descartando a primeira letra escolhida, temos 5 opções para a escolha da segunda letra.

Descartando a primeira e a segunda letras escolhidas, temos 4 opções para escolha da terceira letra.

6.5.4 = 120

Não localizamos a resposta entre as alternativas da questão.

Questão 24. Sabe-se que a probabilidade do João ser admitido em algum curso do ensino superior é de 0,75. Qual é a probabilidade de não ingressar?

a) 0,25

b) 0,35

c) 0,75

d) 0,15

Resolução

João tem apenas duas opções, ser admitido em algum curso superior ou não ser admitido em algum curso superior.

Considerando que 1 representa todas as possibilidades de João, temos:

1 – 0,75 = 0,25

Resposta: A

Questão 25. Lança-se simultaneamente três moedas equilibradas, de duas faces cara e coroa. Qual será a probabilidade de sair pelo menos duas caras?

a) 1

b) 1/2

c) 1/4

d) 3/8

Resolução

Calcularemos a probabilidade de sair pelo menos duas caras, considerando que C representa Cara, e K representa coroa.

• Inicialmente, calcularemos a probabilidade de sair exatamente 3 Caras.

P(C).P(C).P(C) = 1/2 . 1/2 . 1/2 = 1/8

• Calcularemos agora a probabilidade de sair exatamente duas Caras.

P(C).P(C).P(K) = 1/2 . 1/2 . 1/2 = 1/8

Veja que duas caras e uma coroa pode aparecer de 3 formas diferentes, ou seja, a probabilidade de sair exatamente duas caras é dada por:

3 . 1/2 = 3/8

Probabilidade total:

1/8 + 3/8 = 4/8 = 1/2

Resposta: B

Questão 26. Qual das sucessões é convergente?

Resolução

Podemos verificar que a série da letra A é convergente através do teste da razão.

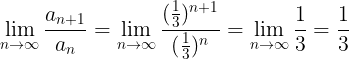
Como 1/3 < 1, a série converge.

Resposta: A

Questão 27. Se (a₁, a₂, a₃) é uma progressão geométrica (PG), cujo primeiro termo é 1 e a soma dos termos é 157, então a razão (q) é igual a

a) -13

b) 12

c) -13 e 12

d) 13 e -12

Resolução

Como estamos tratando de uma progressão geométrica de razão q, os três primeiros termos são:

1, q, q²

Sabendo que a soma é igual a 157:

1 + q + q² = 157

q² + q + 1 – 157 = 0

q² + q – 156 = 0

Temos uma equação do segundo grau.

• Calculando o valor de Delta:

Δ = b² – 4ac

Δ = 1² – 4.1.(-156)

Δ = 1 + 624

Δ = 625

• Calculando o valor de q:

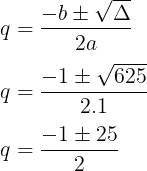
q = -13 ou q = 12

Resposta: C

Questão 28. Qual é a opção correta?

a) Uma função é bijectiva se f(-x) = -f(x)

b) Uma função é ímpar se f(-x) = -f(x)

c) Uma função é injectiva se f(-x) = -f(x)

d) Uma função é par se f(-x) = -f(x)

Resolução

A função seno, por exemplo, é uma função ímpar, pois sen(-x) = – sen(x), porém não é injetora nem sobrejetora, descartando assim as alternativas A e C.

Uma função f é considerada par quando f(x) = f(-x) e ímpar quando f(-x) = -f(x).

Resposta: B

Questão 29. Considere as funções f(x) = log₂(x+1) e g(x) = arccos(x). Qual é o valor de gof(1)?

a) 30°

b) 90°

c) 0°

d) 45°

Resolução

Temos duas funções, f e g, e desejamos calcular o valor da função composta gof(x) aplicada para x = 1.

Calcularemos inicialmente o valor de f(1):

f(1) = log₂(1+1) = = log₂(2) = 1

Calculando o valor de g(1):

g(1) = arccos(1) = 0°

Observe que o arco dentre as alternativas cujo cosseno é igual a 1 é o 0°.

Resposta: C

Questão 30. Qual é o resultado de

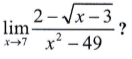
a) 1/4

b) 1/14

c) 1/28

d) 1/56

Resolução

A maioria dos limites fracionários envolvendo radiciação pode ser resolvido multiplicando-se o o conjugado pelo numerador e pelo denominador.

Neste caso, multiplicaremos por 2 + √(x-3):

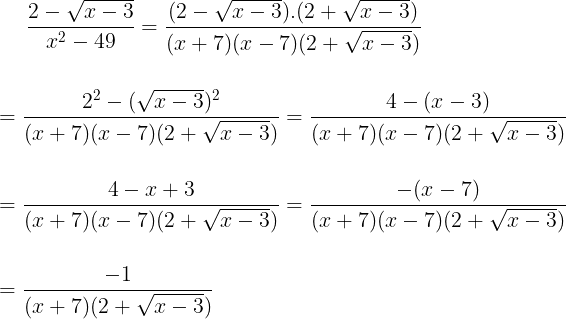
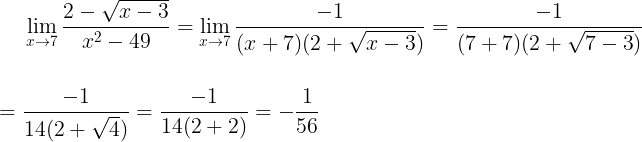
Não existe essa resposta entre as alternativas.

Questão 31. Qual é o resultado de

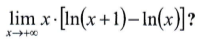
a) 4

b) 1

c) 3

d) 2

Resolução

Utilizando uma das propriedades dos logaritmos:

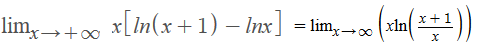
Manipulando a expressão, ao invés de multiplicamos o logaritmo por x, dividiremos por 1/x:

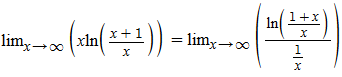
Aplicando a regra de L’Hopital:

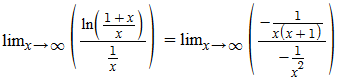
Manipulando as frações:

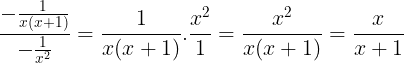
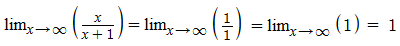
Resposta: B

Questão 32. Qual é o valor de m para que a função seja contínua em x=1?

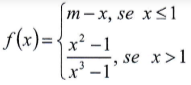
a) 1

b) 2

c) -1

d) -2

Resolução

Observe que (x² – 1)/(x³ – 1) não está definido para x = 1. Neste caso, devemos calcular o valor do limite:

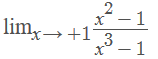
Utilizando os produtos notáveis, podemos fatorar numerador e denominador:

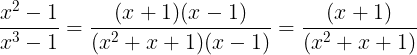
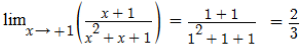
Para que a função seja contínua em x = 1, devemos ter:

m – x = 2/3

m – 1 = 2/3

m = 2/3 + 1

m = 5/3

Não existe essa resposta entre as alternativas.

Questão 33. Sendo f(x) = log₃(x+1) – 2 uma função de ]-1, +∞[ →R, qual é a sua função inversa?

a) f^-1(x) = 3^x-2 + 1

b) f^-1(x) = 3^x-2 – 1

c) f^-1(x) = 3^x+2 – 1

d) f^-1(x) = 3^x+2 + 1

Resolução

Considerando a função, com f(x) = y, temos:

log₃(x+1) – 2 = y

log₃(x+1) = y + 2

Pela definição de logaritmos:

3^{(y + 2)} = x + 1

3^{(y + 2)} – 1 = x

x = 3^{(y + 2)} – 1

Invertendo as variáveis:

f^-1(x) = 3^x+2 – 1

Resposta: C

Questão 34. Qual é a segunda derivada da função f(x) = x³.ln(2x)?

a) f”(x) = 6x.ln(2x) + 5x

b) f”(x) = 6x.ln(2x) + 5

c) f”(x) = 6x.ln(2x) – 5x

d) f”(x) = 6x.ln(2x) + 5x

Resolução

Considerando g(x) = x³ e h(x) = ln(2x), podemos aplicar a regra do produto:

(g.h)’ = g’.h + h’.g

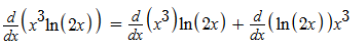
Considerando que:

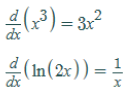
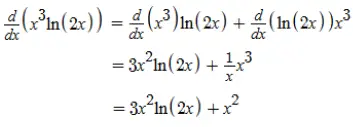
Calcularemos agora a derivada segunda:

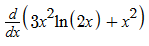
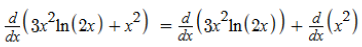
A derivada de x² é 2x.

A derivada de 3x².ln(2x) pode ser calculada pelo mesmo processo da derivada primeira, onde utilizamos a regra do produto.

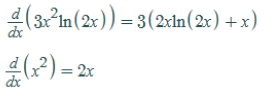
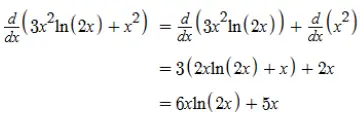
Resposta: A

Questão 35. Quais são os intervalos de monotonia da função

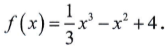
a) f(x) cresce para x∈]-∞, 2[ e decresce para x∈]2, +∞[

b) f(x) cresce para x∈]-∞, 0[ e decresce para x∈]0, +∞[

c) f(x) cresce para x∈]0, 2[ e decresce para x∈]-∞, 0[∪]2, +∞[

d) f(x) cresce para x∈]-∞, 0[∪]2, +∞[ e decresce para x∈]0, 2[

Resolução

A forma mais fácil de verificarmos os intervalos de monotonia de uma função é através da derivação.

Quando a função derivada é positiva, a função é crescente, e quando a função derivada é negativa, a função é decrescente.

f'(x) = x² – 2x

Veja que a derivada é uma função do segundo grau.

Calculando as raízes:

x² – 2x = 0

x(x – 2) = 0

As raízes são 0 e 2.

Como o gráfico de uma função quadrática possui o formato de uma parábola, a>0, e as raízes são 0 e 2, ele terá o seguinte formato:

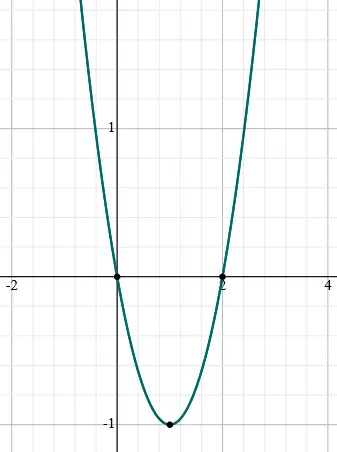
Daí, a função f será crescente para x < 0 ou x > 2, e decrescente para 0 < x < 2.

Resposta: D

Gostou da resolução do Exame de Admissão da UP 2020?

Deixe o seu comentário.