Olá amigos estudantes! A relação fundamental da trigonometria é o nosso assunto de hoje. O objetivo é aprender a utilizar a relação para facilitar a nossa vida nas questões de trigonometria.
Pede-se que o aluno tenha conhecimento prévio sobre triângulos, teorema de Pitágoras e circunferência trigonométrica.
Bom estudo a todos!
A RELAÇÃO FUNDAMENTAL DA TRIGONOMETRIA
Também conhecida como fórmula fundamental da trigonometria, essa fórmula é responsável por relacionar os valores de seno e cosseno de um mesmo ângulo. Veja:
![]()
Reparou a semelhança com o teorema de Pitágoras? Realmente tem tudo a ver, na verdade a fórmula acima é derivada do teorema, fato este que pode ser notado facilmente na circunferência trigonométrica:
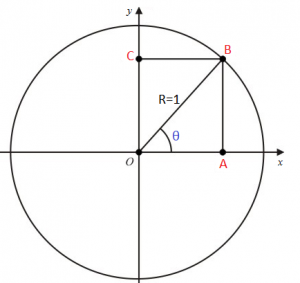
Como a circunferência possui raio igual a 1, temos que a hipotenusa OB = 1. Daí, utilizando as fórmulas do seno e do cosseno, temos que:
senθ = AB/1 = AB
cosθ = OA/1 = OA
Aplicando o teorema de Pitágoras:
AB² + OA² = 1²
sen²θ + cos²θ = 1
Viu como é simples? Agora que você já aprendeu a relação fundamental da trigonometria e de onde ela vem, já podemos analisar alguns exemplos:
Exemplo 1: Calcule o valor aproximado do cosseno de 40º, sabendo que sen40º ≅ 0,64.
sen²θ + cos²θ = 1
sen²40º + cos²40º = 1
(0,64)² + cos²40º ≅ 1
0,41 + cos²40º ≅ 1
cos²40º ≅ 1 – 0,41
cos²40º ≅ 0,59
cos40º ≅ √0,59
cos40º ≅ 0,77
Exemplo 2: Calcule o valor aproximado do cosseno de 30º, sabendo que sen30º = 0,5.
sen²θ + cos²θ = 1
sen²30º + cos²30º = 1
(0,5)² + cos²40º = 1
0,25 + cos²40º = 1
cos²30º = 1 – 0,25
cos²30º = 0,75
cos30º = √0,75
cos30º ≅ 0,87
Exemplo 3: Calcule o valor do sen(45º), sabendo que cos(45º) = √2/2.
sen²θ + cos²θ = 1
sen²45º + cos²45º = 1
sen²45º + (√2/2)² = 1
sen²45º + 2/4 = 1
sen²45º + 1/2 = 1
sen²45º = 1 – 1/2
sen²45º = 1/2
sen45º = √(1/2)
sen45º = 1/√2
sen45º = √2/2
