Qual estudante nunca ouviu falar sobre raiz quadrada? Possivelmente nenhum não é mesmo? Hoje vamos aprender que existem raízes de vários índices. A este conteúdo damos o nome de radiciação, onde vamos veremos a definição, as propriedades e alguns exemplos.

É muito importante que você tenha aprendido o conteúdo de potenciação, pois a radiciação e a potenciação andam juntas, na verdade uma é o inverso da outra.

Bons estudos!

Definição

Dado um número real x não negativo e um número natural n, com n>0, chamamos de raiz enésima aritmética do número real x o número real não negativo y, tal que:

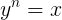
E para representarmos a raiz enésima de x utilizamos a simbologia:

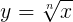
Exemplos

Para quem está estudando o assunto pela primeira vez parece um pouco complicado não é mesmo? Vamos simplificar através de alguns exemplos.

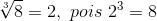
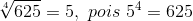
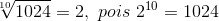
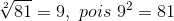
A raiz quadrada

Pela definição de radiciação podemos ver que que o índice da raiz pode ser qualquer número natural maior ou igual a 1, ou seja, podemos ter uma raiz de índice 10, 20 ou 1000, por exemplo. Mas o mais utilizado é o 2, tanto que se convencionou que, quando não utilizamos nenhum valor, esse será o número natural 2. Veja:

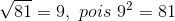
Propriedades da Radiciação

No estudo da radiciação existem 5 propriedades que são muito utilizadas na resolução de exercícios. Vamos falar um pouquinho sobre elas.

Sejam “a” e “b” números reais não negativos, “m” um número inteiro e “n” e “p” números naturais diferentes de zero.

Propriedade 1:

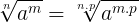
Propriedade 2:

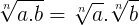
Propriedade 3:

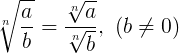
Propriedade 4:

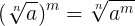
Propriedade 5:

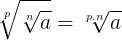
Gostou da nossa publicação sobre a radiciação?

Deixe o seu comentário.