Para você que está se preparando para os principais concursos do país, preparamos uma página super especial. Trata-se de um resumo dos tópicos mais importantes do raciocínio lógico.

Temos certeza que o conteúdo é de grande valia para os alunos que já estão estudando há bastante tempo e que precisam relembrar alguns conteúdos na véspera da prova, assim como os iniciantes, que ainda estão começando a estudar o conteúdo.

Bons estudos!

 

 

1. Proposições:

 

Chamaremos de proposição (ou sentença), o conjunto de palavras ou símbolos que exprimem um pensamento de sentido completo.

 

Exemplos:

a) O carro é azul.

b) A capital do Brasil é Brasília.

c) O Japão está localizado na África.

Observe que as proposições podem ser verdadeiras ou falsas.

 

Princípios:

Existem alguns princípios que regem as proposições. Veja:

 

1 – Princípio da não-contradição:

Uma proposição não pode ser verdadeira e falsa simultaneamente.

 

2 – Princípio do Terceiro Excluído:

Uma proposição só pode ter dois valores verdades, isto é, é verdadeiro (V) ou falso (F), não podendo ter outro valor.

Para simplificar, as proposição costumam ser representadas por letras do alfabeto, maiúsculas ou minúsculas, dependendo do autor.

Podemos ainda combinar duas ou mais proposições. Para isto, utilizaremos alguns operadores (conectivos).

 

Veja:

~ corresponde a “não”

∧ corresponde a “e”

∨ corresponde a “ou”

⇒ corresponde a “então”

⇔ corresponde a “se somente se”

 

Assim, podemos formar novas proposições ao negar uma proposição, como também ao juntar duas ou mais. Veja os tipos:

 

• Conjunções: a ∧ b (lê-se: a e b)

• Disjunções: a ∨ b (lê-se: a ou b)

• Condicionais: a ⇒ b (lê-se: se a então b)

• Bicondicionais: a ⇔ b (lê-se: a se somente se b)

 

Exemplos:

Sejam as proposições:

p = Paulo sabe matemática.

q = Quem sabe matemática é inteligente.

Podemos formar a proposição:

p ⇒q  = Se Paulo sabe matemática, então Paulo é inteligente.

 

 

2. Tabelas verdade

As tabelas verdade apresentam todos os valores possíveis para uma proposição ou uma combinação de proposições.

Veja as tabelas dos principais conectivos:

 

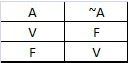
2.1. Negação

A negação da proposição “A” é a proposição “~A”, de maneira que se “A” é verdade então “~A” é falsa, e vice-versa.

 

 

2.2 Conjunção (E)

A conjunção é verdadeira se e somente se ambos os valores são verdadeiros.

 

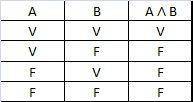
2.3 Disjunção (OU)

A disjunção é falsa se, e somente se ambos os valores forem falsos.

 

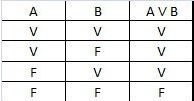
2.4 Condicional (se… então)

A condicional é falsa se, e somente se, o primeiro valor for verdadeiro e o segundo for falso.

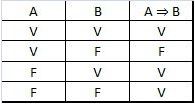
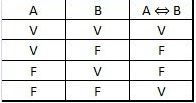
2.5 Bicondicional (se e somente se)

A bicondicional é verdadeira se, e somente se, ambos os valores forem falsos ou ambos verdadeiros.

 

 

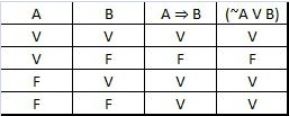
3. Equivalências Lógicas

 

Dizemos que duas proposições compostas são equivalentes quando possuem a mesma tabela verdade. Veja no exemplo abaixo como isto acontece. Temos então que as duas proposições são equivalentes.

Exemplo:

 

 

4. Argumentos

 

Argumento é um conjunto de proposições com uma estrutura lógica de maneira tal que algumas delas acarretam ou tem como conseqüência outra proposição q.

Isto é, o conjunto de proposições p1, p2, p3, . . . , pn que tem como conseqüência outra proposição q.

Chamaremos as proposições p1, p2, p3, . . . , pn de premissas do argumento, e a proposição q de conclusão do argumento.

 

Exemplos:

 

1. Se eu passar no concurso, então irei trabalhar.

Passei no concurso

_____________________________

∴ Irei Trabalhar

 

2. Se ele me ama então casa comigo.

Ele me ama

___________________________

∴ Ele casa comigo

 

3. Todos os brasileiros são humanos.

Todos os paulistas são brasileiro.

_____________________________

∴ Todos os paulistas são humanos

 

4. Se o Palmeiras ganhar o jogo, todos os jogadores receberão o bicho.

Se o Palmeiras não ganhar o jogo, todos os jogadores receberão o bicho.

___________________________________________________

∴ Todos os jogadores receberão o bicho

 

NOTAÇÃO: No caso geral representaremos os argumentos escrevendo as premissas e separando por uma barra horizontal seguida da conclusão com três pontos antes.

 

 

5. Validade de um argumento

 

Conforme citamos anteriormente uma proposição pode ser verdadeira ou falsa. No caso de um argumento diremos que ele é válido ou não válido.

A validade é uma propriedade dos argumentos dedutivos que depende da forma (estrutura) lógica das suas proposições (premissas e conclusões) e não do conteúdo delas. Observe que a validade do argumento depende apenas da estrutura dos enunciados.

 

Exemplo:

Todas as mulheres são bonitas.

Todas as princesas são mulheres.

__________________________________

∴ Todas as princesas são bonitas.

 

Observe que não precisamos de nenhum conhecimento aprofundado sobre o assunto para concluir que o argumento acima é válido. Vamos substituir mulheres, bonitas e princesas por A, B e C respectivamente e teremos:

Todos os A são B.

Todos os C são A.

__________________

∴ Todos os C são B.

 

Logo o que é importante é a forma do argumento e não o conhecimento de A, B e C, isto é, este argumento é válido para quaisquer A, B e C e portanto a validade é consequência da forma do argumento.

O atributo Validade aplica-se apenas aos argumentos dedutivos.

 

 

6. Argumentos Dedutivos e Indutivos

 

Os argumentos são divididos em dois grupos:

 

• Dedutivos

A conclusão é completamente derivada das premissas.

Veja o exemplo abaixo onde as duas premissas provam a conclusão:

Todo ser humano tem mãe.

Todos os homens são humanos.

___________________________

∴ Todos os homens têm mãe.

 

• Indutivos

As premissas não fornecerem o apoio completo para ratificar as conclusões.

Veja o exemplo abaixo onde as 4 premissas não são suficientes para provar a conclusão pois existem outros times.

O Flamengo é um bom time de futebol.

O Palmeiras é um bom time de futebol.

O Vasco é um bom time de futebol.

O Cruzeiro é um bom time de futebol.

_____________________________________________

∴ Todos os times brasileiros de futebol são bons.

 

Portanto nos argumentos indutivos a conclusão possui informações que ultrapassam as fornecidas nas premissas. Sendo assim, não se aplica, então, a definição de argumentos válidos ou não válidos para argumentos indutivos.

 

 

7. Argumentos Dedutivos Válidos

 

Vimos então que a noção de argumentos válidos ou não válidos aplica-se apenas aos argumentos dedutivos, e também que a validade depende apenas da forma do argumento e não dos respectivos valores verdades das premissas. Vimos também que não podemos ter um argumento válido com premissas verdadeiras e conclusão falsa. A seguir exemplificaremos alguns argumentos dedutivos válidos importantes.

 

1) Afirmação do Antecedente

Se p então q

p

__________

∴q

 

Veja o exemplo:

Se José for reprovado no concurso, então será demitido do serviço.

José foi reprovado no concurso.

____________________________________

∴ José será demitido do serviço.

 

2) Negação do Consequente

Se p então q

Não q

__________

∴~p

 

Veja o exemplo:

Se aumentamos os meios de pagamentos, então haverá inflação.

Não há inflação

____________________________________________

∴ Não aumentamos os meios de pagamentos.

 

 

8. Leis de Morgan

 

1. ~(p ∧ q) = ~p ∨ ~q cujo significado é:

“negar a simultaneidade de p e q é afirmar pelo menos não p ou não q”.

 

Ex: Pedro é Mineiro e Paulo é Capixaba.

p = Pedro é Mineiro

q = Paulo é Capixaba

 

Negando-a, temos:

Pedro não é mineiro ou Paulo não é capixaba.

 

2. ~(p ∨ q) = ~p ∧ ~q cujo significado é:

“negar a ocorrência de pelo menos p ou q é afirmar nem p nem q”.

 

Ex: Augusto é feio ou Ana é Bonita.

p = Augusto é feio

q = Ana é bonita

Negando-a, temos:

Augusto não é feio e Maria não é bonita.