Estudando matemática para concursos? Confira aqui várias questões comentadas de matemática da banca Vunesp.
Não deixe de ver também em nosso menu provas resolvidas de concursos organizados pela Vunesp.
Bom estudo!
Questão 1 (TJ SP). Para fazer 200 unidades do produto P, uma empresa utilizou 3/4 do estoque inicial (E) do insumo Q. Para fazer mais 300 unidades do produto P, vai utilizar a quantidade que restou do insumo Q e comprar a quantidade adicional necessária para a produção das 300 unidades, de modo que o estoque do insumo Q seja zerado após a produção desse lote. Nessas condições, deverá ser comprada, do insumo Q, uma quantidade que corresponde, do estoque inicial E, a
(A) 3/8.
(B) 9/8.
(C) 7/8.
(D) 1/4.
(E) 2/3.
Resolução
Podemos montar duas equações:
“Para fazer 200 unidades do produto P, uma empresa utilizou 3/4 do estoque inicial (E) do insumo Q.”
200 = E.3/4
“Para fazer mais 300 unidades do produto P, vai utilizar a quantidade que restou do insumo Q e comprar a quantidade adicional necessária para a produção das 300 unidades, de modo que o estoque do insumo Q seja zerado após a produção desse lote.”
300 = E.1/4 + X
Onde:
x é a quantidade que deve ser comprada
E é o estoque inicial
Pela primeira equação temos:
E.3/4 = 200
E = 800/3
Pela segunda equação, e sabendo que E = 800/3 temos:
300 = (800/3) . (1/4) + X
300 = 200/3 + X
x = 300 – 200/3
x = 700/3
Finalizando:
x/E = (700/3) / (800/3) = 7/8
Resposta: C
Questão 2 (PM SP). Uma pessoa foi a uma papelaria com R$ 20,00 para comprar canetas, todas de mesmo preço. Ao chegar à papelaria, constatou que, se comprasse 4 canetas e um bloco de anotações gastaria exatamente os R$ 20,00, mas se quisesse comprar somente 6 canetas, não seria possível, pois ficaria faltando R$ 1,00. O valor do bloco de anotações era (em reais)
a) 4,50
b) 5,50
c) 6,00
d) 4,00
e) 5,00
Resolução
Orçamento de 20 reais
Quando a pessoa tentou comprar 6 canetas, faltou 1 real, ou seja, 6 canetas custam R$ 21 reais.
Calculando o valor de cada caneta
21 / 6 = 3,50
Calculando o valor de 4 canetas
4 x 3,5 = 14,00
Como 1 bloco + 4 canetas custam exatamente 20 reais, e 4 canetas custam 14 reais, podemos concluir que o bloco custa:
20 – 14 = 6,00
Resposta: C
Questão 3 (TJ SP). A figura seguinte, cujas dimensões estão indicadas em metros, mostra as regiões R1 e R2, ambas com formato de triângulos retângulos, situadas em uma praça e destinadas a atividades de recreação infantil para faixas etárias distintas.
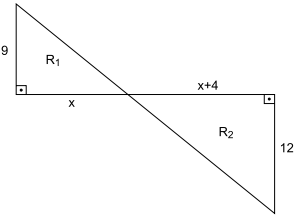
Se a área de R1 é 54 m², então o perímetro de R2 é, em metros, igual a
(A) 40.
(B) 42.
(C) 54.
(D) 48.
(E) 36.
Resolução
Sabendo que a área de R1 é 54m², temos:
9.x/2 = 54
x = 54.2/9
x = 12
Como um dos lados de R2 mede x+4, a medida real é de 16 m.
Vamos agora utilizar o teorema de pitágoras para calcular a hipotenusa do triângulo R2:
h² = 16² + 12²
h² = 256 + 144
h² = 400
h = 20 m
Calculando o perímetro de R2:
12 + 16 + 20 = 48 m
Resposta: D
Questão 4 (TJ SP). Norberto tomou dois empréstimos, que foram pagos após 2 meses com o acréscimo de juro simples. No primeiro, de certo valor, a taxa de juros foi de 1% ao mês. No segundo, de valor R$ 1.600,00 maior que o do primeiro, a taxa de juros foi de 1,5% ao mês. Sabendo que a soma dos juros pagos nos dois empréstimos foi igual a R$ 128,00, é correto afirmar que a soma dos valores desses dois empréstimos é igual a
(A) R$ 3.600,00.
(B) R$ 4.600,00.
(C) R$ 4.800,00.
(D) R$ 3.200,00.
(E) R$ 4.000,00.
Resolução
Primeiro empréstimo:
Valor x;
juros simples de 1% a.m.;
prazo de 2 meses;
Segundo empréstimo:
Valor (x + 1600);
juros simples de 1,5% a.m.;
prazo de 2 meses;
Lembrando que nos juros simples, não existem os chamados “juros sobre juros”, vamos calcular os juros pagos:
Primeiro empréstimo:
x.0,01.2 = 0,02.x
Segundo empréstimo:
(x + 1600).0,015.2 = (x + 1600).0,03 = 0,03x + 1600.0,03 = 0,03x + 48
Como os juros totais foram de 128, podemos montar a seguinte equação:
0,02.x + 0,03x + 48 = 128
0,05x = 128 – 48
0,05x = 80
x = 80/0,05
x = 1600
Concluímos então que o primeiro empréstimo foi de 1600 e o segundo de 3200.
Daí, o total foi de 4800.
Resposta: C
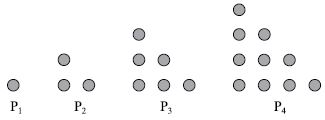
Questão 5 (SAP – SP). Observe a sequência de figuras com bolinhas.
Mantendo-se essa lei de formação, o número de bolinhas na 13.a posição (P13) será de
(A) 91.
(B) 74.
(C) 63.
(D) 58.
(E) 89.
Resolução
Veja que:
P1 = 1
P2 = 1 + 2
P3 = 1 + 2 + 3
…
P13 = 1 + 2 + 3 + … + 12 + 13
Basta somarmos os termos dessa PA, onde a1 = 1, a13 = 13 e n = 13
Pela fórmula da soma de uma PA:
S = (a1 + an).n/2
S = (1 + 13). 13/2
S = 14.13/2
S = 91
Resposta: A
Questão 6 (TJ SP). Uma barra de madeira maciça, com a forma de um paralelepípedo reto retângulo, tem as seguintes dimensões: 48 cm, 18 cm e 12 cm. Para produzir calços para uma estrutura, essa barra deve ser cortada pelo carpinteiro em cubos idênticos, na menor quantidade possível, sem que reste qualquer pedaço de barra. Desse modo, o número de cubos cortados será igual a
a) 54
b) 52
c) 50
d) 48
e) 46
Resolução
Veja que precisamos dividir 48, 18 e 12 pelo mesmo número, e na menor quantidade possível, ou seja, os pedaços devem ter o maior tamanho possível.
Devemos então calcular o MDC de 48, 18 e 12, que é 6.
Logo:
O lado que mede 48cm será dividido em 48/6 = 8
O lado que mede 18cm será dividido em 18/6 = 3
O lado que mede 12cm será dividido em 12/6 = 2
Total de cubos: 8x3x2 = 48
Resposta: D
Questão 7 (TJ SP). Certo capital foi aplicado a juros simples, à taxa de 1,5% ao mês. Para que seja possível resgatar um montante igual a 7/4 do capital inicial, o tempo mínimo que esse capital deverá permanecer aplicado é:
(A) 3 anos e 4 meses.
(B) 3 anos e 9 meses.
(C) 4 anos e 2 meses.
(D) 2 anos e 8 meses.
(E) 2 anos e 10 meses.
Resolução
Temos que 7/4 = 1,75
Utilizando a fórmula de juros simples:
M = C.(1 + in), onde:
M = Montante (1,75.C)
C = Capital inicial (C)
i = taxa (0,015)
n = prazo em meses
1,75C = C.(1 + 0,015.n)
1,75 = (1 + 0,015.n)
1,75 – 1 = 0,015.n
0,75 = 0,015.n
n = 0,75/0,015
n = 50 meses
Note que 48 meses equivale a 4 anos.
Resposta 4 anos e 2 meses.
Resposta: C
Questão 8 (PC SP). Em uma empresa com 5 funcionários, a soma dos dois menores salários é R$ 4.000,00, e a soma dos três maiores salários é R$ 12.000,00. Excluindo-se o menor e o maior desses cinco salários, a média dos 3 restantes é R$ 3.000,00, podendo-se concluir que a média aritmética entre o menor e o maior desses salários é igual a
(A) R$ 3.500,00.
(B) R$ 3.400,00.
(C) R$ 3.050,00.
(D) R$ 2.800,00.
(E) R$ 2.500,00.
Resolução
Sejam os salários em ordem crescente: x, y, z, w, k
Temos:
x + y = 4000
z + w + k = 12000
(y + z + w)/3 = 3000, ou seja, y + z + w = 9000
Somando as duas primeiras equações:
x + y + z + w + k = 16000
Subtraindo a terceira equação da soma acima:
x + y + z + w + k – y – z – w = 16000 – 9000
x + k = 7000
Como x é o menor e k é o maior salário, concluímos que a média é 3500.
Resposta: A
Gostou das nossas questões comentadas de matemática da Vunesp?
Deixe o seu comentário.