Confira aqui várias questões comentadas de matemática, elaboradas pela banca NUCEPE, para você se preparar para as próximas provas de concursos públicos.
Bom estudo!
Questão 1 (Guarda Civil – Teresina). Considerando os conjuntos: ℝ (números reais), ℝ\ℚ (números irracionais), ℚ (números racionais), ℤ (números inteiros) e ℕ (números naturais). Qual das seguintes afirmações não é verdadeira?
a) ℝ⋃(ℝ\ℤ)=ℝ
b) (ℕ⋃ℤ)⋃(ℚ⋃ℝ\ℚ)=ℝ
c) ℕ⋂ℤ=ℕ
d) ℚ⋃ℤ⋃ℕ=ℝ
e) (ℕ⋃ℚ)⋂ℝ=ℚ
Resolução
O conjunto dos números reais (ℝ) é a união do conjunto dos números racionais com o conjunto dos números irracionais.
Observe que a igualdade ℚ⋃ℤ⋃ℕ=ℝ não é verdadeira pois não temos o conjunto dos números irracionais.
Resposta: D
Questão 2 (Guarda Civil – Teresina). A esposa de um matemático pede para ele comprar pães, e a quantidade de pães a ser comprada está escrita em um bilhete que ela entrega a ele. Ao chegar na padaria, o matemático abre o bilhete e está escrito:
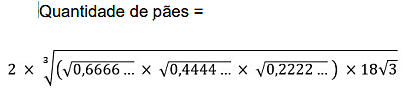
Qual a quantidade de pães que a esposa do matemático pediu para ele comprar?
a) 2
b) 4
c) 6
d) 8
e) 10
Resolução
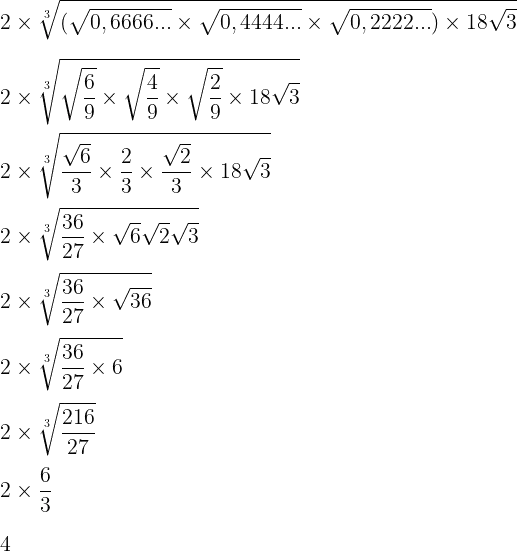
Resposta: B
Questão 3 (Bombeiros – PI). Inflação é nada mais nada menos que a perda do valor do dinheiro. Pareceu fácil demais esta definição? Bom, vamos então expandir sua visão! A inflação é quando o valor do dinheiro é desvalorizado assim diminuindo seu poder de compra, como no exemplo: Todo mês um trabalhador recebe R$100,00 por seu trabalho e com este dinheiro compra um saco de feijão por R$10,00. Nos jornais é anunciado que a inflação deste país é de 10% ao mês. No mês seguinte, este mesmo trabalhador quando for comprar seu saco de feijão vai encontrar seu preço a R$11,00. Mas porque houve este aumento? O que houve foi que a inflação reajustou o valor do alimento em 10% (10% x R$10,00 = R$1,00) enquanto que o salário do trabalhador manteve-se em seu valor antigo. Podemos assim concluir que o poder de compra deste trabalhador diminuiu devido ao aumento do preço dos alimentos.
Disponível em: http://economiasemsegredos.com/o-que-e-inflacao-como-calcular. Acesso em 10/10/2017.
Se no exemplo acima o trabalhador tivesse um aumento salarial de 4,5%, qual seria a perda do seu poder de compra?
A) 5%
B) 5,5%
C) 6%
D) 6,5%
E) 10%
Resolução
Observe que o salário do trabalhador foi valorizado em 4,5%, enquanto a inflação foi de 10%.
Podemos utilizar a fórmula da taxa real:
(1 + in) = (1 + ir).(1 + if)
Onde:
in = taxa nominal = 4,5%
ir = taxa real = ?
if = taxa inflação = 10%
(1 + in) = (1 + ir).(1 + if)
1 + 0,045 = (1 + ir).(1 + 0,10)
1,045 = (1 + ir).(1,1)
(1 + ir) = 1,045 / 1,1
(1 + ir) = 0,95
ir = 0,95 – 1
ir = – 0,05 (inflação de 5%)
Resposta: A
Questão 4 (Bombeiros – PI). Uma guarnição do corpo de bombeiros é formada de 6 sargentos, dentre eles João; 20 soldados, sendo um deles Emanuel. O comando geral pretende formar uma turma com 3 sargentos e 4 soldados para fazer um curso de especialização em resgate causado por terremotos. Sabendo que o sargento João já tem direito adquirido para fazer o curso e que, por problemas particulares, o soldado Emanuel não vai poder participar, de quantas maneiras diferentes o comando geral pode montar essa turma de especialização?
A) 116280.
B) 96900.
C) 77520.
D) 48450.
E) 38760.
Resolução
Seriam escolhidos 3 entre 6 sargentos, porém o João já está escolhido, ou seja, temos uma combinação de 5, tomados 2 a 2:
C5,2 = 5!/(5-2)!2! = 5!/3!2! = 10
Seriam escolhidos 4 entre 20 soldados, porém o Emanuel não poderá participar, ou seja, temos uma combinação de 19, tomados 4 a 4:
C19,4 = 19!/(19-4)!4! = 19!/15!4! = 3.876
Total
10 x 3876 = 38.760
Resposta: E
Questão 5 (Prefeitura de Teresina). Sendo p/q a fração irredutível equivalente a 0,0222… / 0,001818… Qual o valor de p – q?
a) 92.
b) 99.
c) 100.
d) 101.
e) 110.
Resolução
O número 0,222… é uma dízima periódica que equivale a fração 2/9, ou seja, o numerador 0,0222… equivale a fração 2/90, por ser 10 vezes menor.
O número 0,1818… também é uma dízima periódica, e equivale a fração 18/99, ou seja, o denominador 0,001818… equivale a fração 18/9900.
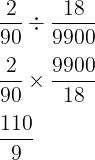
Calculando p – q:
110 – 9 = 101
Resposta: D
Questão 6 (Prefeitura de Teresina). A figura a seguir é formada por quatro triângulos unidos pelos vértices nos quais estão em destaque, na cor cinza, alguns ângulos internos.
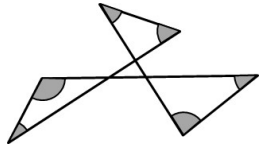
Qual a soma dos ângulos internos em destaque?
a) 180º.
b) 270º.
c) 360º.
d) 540º.
e) 720º.
Resolução
Observe na figura abaixo que os ângulos com a mesma cor são opostos pelo vértice, e por consequência, são congruentes.
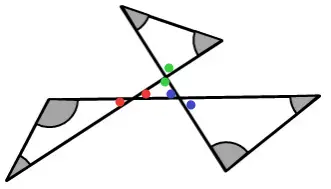
A soma dos ângulos internos de um triângulo é igual a 180°, ou seja, a soma dos ângulos internos dos três maiores triângulos é igual a:
3 x 180° = 540°
Podemos calcular a soma dos ângulos internos em destaque subtraindo a soma dos ângulos coloridos de 540°.
Observe no triângulo do meio que a soma dos ângulos coloridos é igual a 180°, ou seja, podemos calcular a soma buscada pela questão através da subtração:
540º – 180º = 360º
Resposta: C
Questão 7 (PM Piauí). O número de um cartão de crédito consiste de uma lista ordenada de quinze dígitos,
escolhidos entre os dígitos de zero a nove. Para certo cartão, a soma de cada quatro dígitos
consecutivos é vinte e alguns dos dígitos do cartão estão assinalados a seguir:
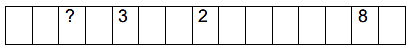
Qual dígito ocupa a terceira posição (da esquerda para a direita) no número deste cartão?
A) 2
B) 3
C) 7
D) 8
E) 9
Resolução
Considerando que a soma de cada quatro dígitos consecutivos é sempre igual a 20, podemos concluir que o mesmo dígito se repete a cada quatro posições. Veja porque:

Nas primeiras quatro casas:
A + B + C + D = 20
Da segunda a quinta casa:
B + C + D + E = 20
Subtraindo-se a primeira da segunda equação:
A + B + C + D – (B + C + D + E) = 20 – 20
A + B + C + D – B – C – D – E = 0
A – E = 0
A = E
Veja que o primeiro dígito é igual ao quinto dígito. É possível concluir da mesma forma que isto vale para todos, ou seja, o mesmo dígito se repete a cada quatro posições.
Com essas informações, é possível descobrir vários dígitos do cartão de crédito:

A questão quer saber o dígito da terceira casa, que será representado por x. Como a soma dos quatro primeiros dígitos é igual a 20, temos que:
3 + 8 + x + 2 = 20
x + 13 = 20
x = 20 – 13
x = 7
Resposta: C
Questão 8 (PM – Piauí). Se x homens, trabalhando x horas por dia, durante x dias, constroem um muro com x metros de comprimento, qual o comprimento, em metros, do mesmo tipo de muro, que será construído por y homens, de mesma capacidade de trabalho que os anteriores, trabalhando y horas por dia, durante y dias? Admita que x e y são inteiros positivos.
A) y
B) y² /x
C) x³ /y²
D) x² /y
E) y³ /x²
Resolução
A questão pode ser resolvida através da regra de três composta, onde consideraremos que k representa o comprimento que será construído por y homens, durante y horas por dia e y dias.
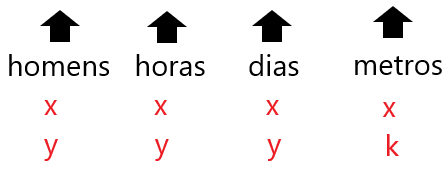
Quanto maior a quantidade de homens, horas ou dias, maior será a quantidade de metros, ou seja, são grandezas diretamente proporcionais.
x/k = (x/y) . (x/y) . (x/y)
x/k = x³ / y³
1/k = x² / y³
k = y³ / x²
Resposta: E
Questão 9 (PM – Piauí). Toda a produção semanal de latas de suco de certa fábrica foi vendida a três lojas, aqui designadas por A, B e C. Para a loja A, foi vendido um terço da produção, para a loja B, foi vendido 40% da produção, e, para a loja C, foram vendidas 11.360 unidades. Qual a produção semanal de latas de suco dessa fábrica?
A) 42.000 latas.
B) 42.300 latas.
C) 42.420 latas.
D) 42.540 latas.
E) 42.600 latas.
Resolução
Seja x a quantidade de latas produzidas na semana.
Temos que:
A loja A recebeu x/3 latas.
A loja B recebeu 0,4x latas.
A loja C recebeu 11360 latas.
x/3 + 0,4x + 11360 = x
3(x/3 + 0,4x + 11360) = 3.x
x + 1,2x + 34080 = 3x
34080 = 3x – x – 1,2x
0,8x = 34080
x = 34080/0,8
x = 42600
Resposta: E
Questão 10 (PM – Piauí). Uma praça é formada por um retângulo e dois semicírculos com diâmetros justapostos ao lado menor do retângulo. Os lados do retângulo medem 40 m e 30 m. Uma calçada com 3 m de largura deve ser construída em torno de uma praça. Qual o valor total a ser pago por essa calçada, se o metro quadrado do pavimento é de R$ 30,00? A seguir, temos uma ilustração da situação, fora de escala. Obs.: adote a aproximação π ≃ 3,14.
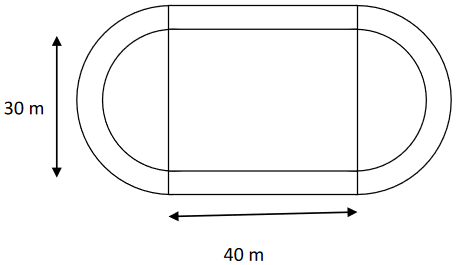
A) R$ 16.525,40
B) R$ 16.525,50
C) R$ 16.525,60
D) R$ 16.525,70
E) R$ 16.525,80
Resolução
Vamos calcular a área da calçada em duas etapas.
- No retângulo, temos 80 metros (40 + 40) de calçada:
80 x 3 = 240 m²
- Dois semicírculos geram um círculo completo. A área da calçada neste caso é a área da coroa circular representada pela diferença entre a área de uma circunferência de raio igual a 18 m e a área de uma circunferência de raio igual a 15 m.
π.18² – π.15² = π.(324 – 225) = 3,14.99 = 310,86 m²
Área total:
240 + 310,86 = 550,86 m²
Como cada m² custa 30 reais:
550,86 . 30 = 16.525,80
Resposta: E
Gostou da nossa seleção de questões de matemática comentadas da NUCEPE?
Deixe o seu comentário.

Sim. Quero adquirir as questões.
Você pode comprar as questões através deste link.
https://go.hotmart.com/N59352527L