Procurando questões comentadas sobre matemática da banca Cespe? Chegou ao site certo. Aqui você encontra milhares de exercícios resolvidos e comentados.
Não deixe de acessar também em nosso menu os exercícios resolvidos por conteúdo.
Boa sorte!
Questão 1 (PM MA 2017). Na preparação de uma ação policial, um agente fez algumas medições em uma casa noturna, mostradas na figura a seguir. O agente, em pé no ponto A, de frente para a casa noturna, estava a 10 m de distância do ponto C, correspondente à porta de entrada da casa noturna. Do ponto B, posição dos olhos do agente, ele visualizava uma câmera de segurança no ponto D, no prédio da casa noturna, segundo um ângulo de visão de 30 graus com a horizontal.
Perpendicularmente a AC, e a 24 m de A, ficava localizada uma base móvel para apoio à operação, no ponto E.
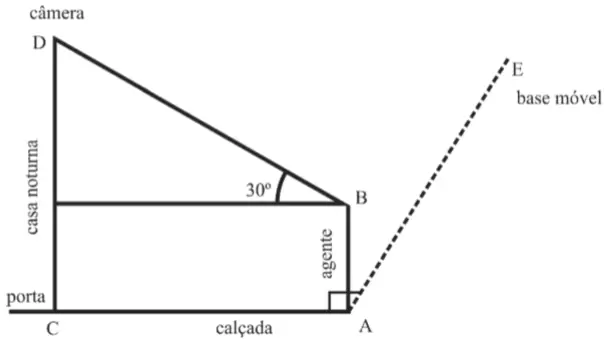
Com referência às informações contidas na situação hipotética e na figura anteriormente apresentadas, julgue a seguinte afirmação:
“Considerando que AB seja igual a 1,70 m, que essa seja a altura dos olhos do agente e que 0,58 seja o valor aproximado para tg30º, então a câmera estava a uma altura inferior a 7 m.”
Resposta: ERRADO
Inserindo as informações do enunciado na figura:
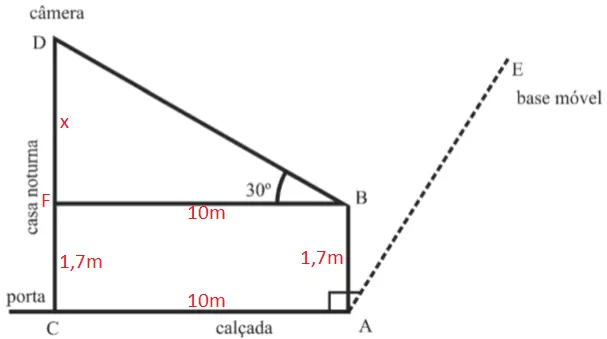
Aplicando a fórmula da tangente no triângulo retângulo BDF, onde x é a diferença entre a altura da câmera e a altura dos olhos do policial:
tg 30º = cateto oposto / cateto adjacente
0,58 = x / 10
x = 10 . 0,58
x = 5,8 m
Adicionando a altura dos olhos do policial:
5,8 + 1,7 = 7,5 m
Questão 2 (TRT ES 2013). Considerando que, na fruteira da casa de Pedro, haja 10 uvas, 2 maçãs, 3 laranjas, 4 bananas e 1 abacaxi, julgue a seguinte afirmação:
Há mais de 1.330 maneiras distintas de Pedro escolher pelo menos uma fruta entre aquelas que estão em sua fruteira.
Resolução
Pedro vai escolher algumas frutas. Ele tem a opção de pegar uma, duas ou várias.
Vamos analisar quantas opções ele tem para cada fruta:
Uva: Pode pegar de 0 a 10, ou seja, 11 opções.
Maçã: Pode pegar de 0 a 2, ou seja, 3 opções.
Laranja: Pode pegar de 0 a 3, ou seja, 4 opções.
Banana: Pode pegar de 0 a 4, ou seja, 5 opções.
Abacaxi: Pode pegar 0 ou 1, ou seja, 2 opções.
Total de opções: 11 x 3 x 4 x 5 x 2 = 1320
Basta descontar a possibilidade de Pedro não pegar nenhuma fruta:
1320 – 1 = 1319
Há 1319 maneiras distintas, ou seja, menos de 1330.
Resposta: ERRADO
Questão 3 (PRF 2013). Considere que o nível de concentração de álcool na corrente sanguínea, em g/L, de uma pessoa, em função do tempo t, em horas, seja expresso por N = – 0,008(t² – 35t + 34). Considere, ainda, que essa pessoa tenha começado a ingerir bebida alcoólica a partir de t = t0 (N(t0 = 0), partindo de um estado de sobriedade, e que tenha parado de ingerir bebida alcoólica em t = t1, voltando a ficar sóbria em t = t2.
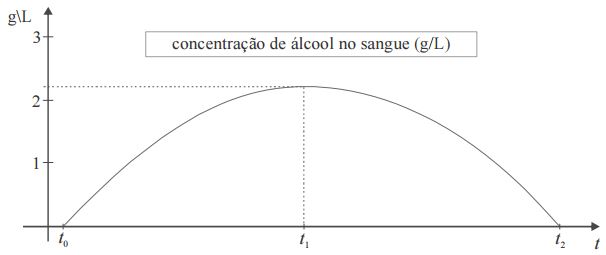
Considere, por fim, a figura acima, que apresenta o gráfico da função N(t) para t є [t0, t2]. Com base nessas informações e tomando 24,3 como valor aproximado de √589, julgue os itens a, b e c.
a) O nível de concentração de álcool na corrente sanguínea da pessoa em questão foi superior a 1 g/L por pelo menos 23 horas.
Resolução
Isso ocorre quando:
– 0,008(t² – 35t + 34) > 1
– 8(t² – 35t + 34) > 1000
t² – 35t + 34 > – 125
t² – 35t + 159 > 0
Δ = b² – 4ac = 35² – 4.1.159 = 589
t = (35 + 24,3)/2 ou t = (35 – 24,3)/2
t = 29,65 ou t = 5,35
S = {5,35 ˂ x ˂ 29,65} , diferença entre eles = 24,3
Resposta: CERTO
b) O valor de t2 é inferior a 36.
Resolução
Basta calcularmos as raízes da função:
-0,008(t² – 35t + 34) = 0 (x 1000)
-8(t² – 35t + 34) = 0 (: -8)
t² – 35t + 34 = 0
t0 = 1 ou t2 = 34
Resposta: CERTO.
c) O nível de concentração mais alto de álcool na corrente sanguínea da referida pessoa ocorreu em t = t1, com t1 > 18 horas.
Resolução
O nível mais alto, em se tratando de uma função do segundo grau, é exatamente a média aritmética das duas raízes 1 e 34.
(1 + 34)/2 = 35/2 = 17,5
Resposta: ERRADO
Questão 4 (Caixa 2006). O Financiamento de Veículos CAIXA é uma linha de crédito exclusiva para quem é cliente há pelo menos 1 ano. Com ele, você compra seu carro novo ou usado nas melhores condições do mercado, com até R$ 35 mil de crédito. As prestações são mensais e calculadas pela Tabela Price.
Mais vantagens:
< taxas de juros reduzidas e pré-fixadas;
< financiamento em até 36 meses;
< financiamento de carros novos ou usados, com até 5 anos de fabricação;
< financiamento de até 85% do valor do veículo.
Amortização:
< é permitida a amortização parcial ou a quitação antecipada do saldo devedor.
Suponha que Marta, cliente da CAIXA há mais de 1 ano, deseja financiar em 24 meses, pelo sistema acima, a compra de um veículo novo de valor igual a R$ 20.000,00. Assuma também que a única taxa cobrada pela CAIXA nesse tipo de financiamento é a taxa de juros pré-fixada de 1% ao mês. Nessa situação e considerando as informações relativas ao financiamento de veículos apresentadas acima, julgue os itens seguintes.
a) As prestações calculadas segundo a Tabela Price são diretamente proporcionais ao montante a ser financiado. Assim, se Marta financiar R$ 14.000,00 para a compra do veículo, a prestação mensal a ser paga será o dobro da que ela pagaria se financiasse apenas R$ 7.000,00.
CORRETO
No sistema PRICE, quando o valor do financiamento dobra, o valor da prestação também dobra.
b) Pelo sistema acima, é de R$ 17.000,00 o valor máximo do financiamento que Marta poderá fazer na CAIXA para pagar o veículo.
CORRETO
Observando que Marta se encaixa nas condições da linha, devemos apenas calcular 85% de 20000:
![]()
Questão 5 (Bombeiros ES). Um soldado, um sargento e um tenente têm suas idades, em anos, dispostas em progressão geométrica, sendo o soldado o mais novo dos três, e o tenente, o mais velho. Sabendo que o produto dessas idades, em anos, é 27.000 e que a soma das idades do sargento e do tenente é 75 anos, julgue os itens a, b e c.
Resolução
Sabendo que as idades do soldado, do sargento e do tenente estão em progressão geométrica, nesta ordem, as idades dos mesmos serão:
Soldado = x/y
Sargento = x
Tenente = xy
onde y é a razão da PG.
Sabendo que o produto das idades é 27000:
x/y . x . xy = 27000
x³ = 27000
x = 30
Sabendo que a idade do sargento é 30, e que a soma das idades do sargento mais tenente é 75, temos que a idade do tenente é 45, ou seja,
xy = 45
30y = 45
y = 45/30
y = 1,5
Calculando a idade do soldado:
x/y = 30/1,5 = 20
Assim:
Soldado: 20 anos
Sargento: 30 anos
Tenente: 45 anos
a) A idade do sargento é superior a 32 anos.
ERRADO
b) Se o tenente fosse 5 anos mais novo, as idades dos três militares, em anos, estariam em progressão aritmética.
CERTO
Se o tenente fosse 5 anos mais novo teríamos:
20, 30, 40 (PA de razão 10)
c) A soma das idades do soldado e do sargento é inferior a 48 anos.
ERRADO
Soldado + Sargento = 50
Questão 6 (SEJUS ES). Considerando uma função real f: R⇒R que satisfaça à condição f(x+1) = 1/f(x), para cada x∈R, julgue os seguintes itens.
a) Se uma f função satisfaz a essa condição, então f(-2) = f(2).
CORRETO.
Vamos utilizar basicamente a relação f(x+1) = 1/f(x).
a) f(2) = f(1+1) = 1/f(1)
b) f(1) = f(0+1) = 1/f(0)
c) f(0) = f(-1+1) = 1/f(-1)
d) f(-1) = f(-2+1) = 1/f(-2)
Temos 4 relações, vamos substituir uma na outra, começando por a até chegar em d:
f(2) = 1/f(1) = 1/1/f(0) = f(0) = 1/f(-1) = 1/1/f(-2) = f(-2)
b) Se, em um sistema de coordenadas cartesianas ortogonais xOy, o gráfico de f for uma reta, então essa reta é paralela ao eixo Ox.
CORRETO
Pelo exercício anterior, temos f(2) = f(0) = f(-2).
Na hipótese do gráfico ser uma reta, ela deve passar obrigatoriamente pelos 3 pontos que são colineares, ou seja, será paralela ao eixo Ox.
Questão 7 (PM CE 2012). Considere que uma viatura policial adquirida por R$ 80.000,00 se desvalorize à taxa composta de 5% ao ano. Nesse caso, considerando-se 0,6 como valor aproximado para 0,9510, é correto afirmar que, 10 anos após a compra, a viatura valerá menos de R$ 45.000,00.
Resolução
Quando falamos que se desvaloriza 5% ao ano, estamos dizendo que a cada ano ela vale 95% do ano anterior, ou seja:
No primeiro ano vale 80000.0,95
No segundo ano vale 80000.0,95²
e assim sucessivamente…
Após 10 anos:
80000.0,9510 = 80000.0,6 = 48000
ERRADO
Gostou das questões comentadas de matemática do Cespe?
Curta e compartilhe nas redes sociais.
